某校为了鼓励在数学竞赛中获奖的学生,准备买若干本课外读物送给他们,如果每人送3本,则还剩8本;如果每人送5本,则最后一人得到的课外读物不足3本,求该校的获奖人数及所买的课外读物的本数?
(本小题满分12分)
某工厂现有80台机器,每台机器平均每天生产384件产品,现准备增加一批同类机器以提高生产总量,在试生产中发现,由于其他生产条件没变,因此每增加一台机器,每台机器平均每天将少生产4件产品.
(Ⅰ)如果增加x台机器,每天的生产总量为 件,请你写出
件,请你写出 与
与 之间的关系式;
之间的关系式;
(Ⅱ)增加多少台机器,可以使每天的生产总量最大?最大生产总量是多少?
(本小题满分12分)
已知函数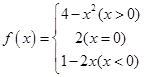 ,
,
(Ⅰ)画出函数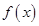 图像;
图像;
(Ⅱ)求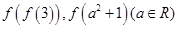 的值;
的值;
(Ⅲ)当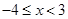 时,求
时,求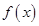 取值的集合.
取值的集合.
(本小题满分12分)
已知函数
(Ⅰ) 判断函数f(x)的奇偶性并证明。
(Ⅱ) 利用单调性定义证明函数f(x)在 上的单调性,并求其最值。
上的单调性,并求其最值。
. (本小题满分10分)
设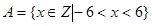 ,
,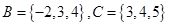 ,求:
,求:
(Ⅰ) ;
;
(Ⅱ)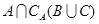
已知函数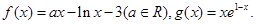
(1)若函数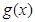 图象在(0,0)处的切线也恰为
图象在(0,0)处的切线也恰为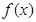 图象的一条切线,求实数a的值;
图象的一条切线,求实数a的值;
(2)是否存在实数a,对任意的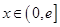 ,都有唯一的
,都有唯一的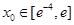 ,使得
,使得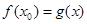 成立,若存在,求出a的取值范围;若不存在,请说明理由。
成立,若存在,求出a的取值范围;若不存在,请说明理由。