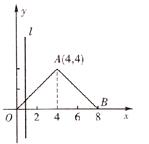
如图所示,直线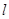 ⊥
⊥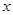 轴,从原点开始向右平行移动到
轴,从原点开始向右平行移动到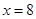 处停止,它截△AOB所得左侧图形的面积为S,它与x轴的交点为
处停止,它截△AOB所得左侧图形的面积为S,它与x轴的交点为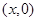 .
.
(1)求函数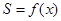 的解析式;
的解析式;
(2)解不等式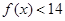 .
.
如图,渔船甲位于岛屿 的南偏西
的南偏西 方向的
方向的 处,且与岛屿
处,且与岛屿 相距12海里,渔船乙以10海里/小时的速度从岛屿
相距12海里,渔船乙以10海里/小时的速度从岛屿 出发沿正北方向航行,若渔船甲同时从
出发沿正北方向航行,若渔船甲同时从 处沿北偏东
处沿北偏东 的方向追赶渔船乙,刚好用2小时追上.
的方向追赶渔船乙,刚好用2小时追上.
(1)求渔船甲的速度;
(2)求 的值.
的值.
求满足下列条件的直线方程:
(1)经过点 ,且与直线
,且与直线 垂直;
垂直;
(2) 经过点 ,且在两坐标轴上的截距相等.
,且在两坐标轴上的截距相等.
(本小题满分14分)
已知函数 ,(
,( e为自然对数的底数)
e为自然对数的底数)
(Ⅰ)当a=1时,求函数f(x)的单调区间;
(Ⅱ)若函数f(x)在 上无零点,求a的最小值;
上无零点,求a的最小值;
(III)若对任意给定的 ,在
,在 上总存在两个不同的
上总存在两个不同的 ,使得
,使得 成立,求a的取值范围.
成立,求a的取值范围.
(本小题满分13分)若集合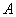 具有以下性质:①
具有以下性质:①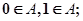 ②若
②若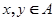 ,则
,则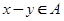 ,且
,且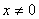 时,
时,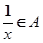 .则称集合
.则称集合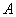 是“好集”.
是“好集”.
(Ⅰ)分别判断集合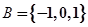 ,有理数集Q是否是“好集”,并说明理由;
,有理数集Q是否是“好集”,并说明理由;
(Ⅱ)设集合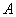 是“好集”,求证:若
是“好集”,求证:若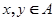 ,则
,则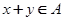 ;
;
(Ⅲ)对任意的一个“好集”A,分别判断下面命题的真假,并说明理由.
命题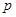 :若
:若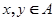 ,则必有
,则必有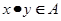 ;
;
命题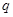 :若
:若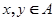 ,且
,且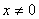 ,则必有
,则必有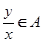 ;
;
(本小题满分12分)在第9届校园文化艺术节棋类比赛项目报名过程中,我校高二(2)班共有16名男生和14名女生预报名参加,调查发现,男、女选手中分别有10人和6人会围棋.
(I)根据以上数据完成以下2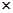 2列联表:
2列联表:
| 会围棋 |
不会围棋 |
总计 |
|
| 男 |
|||
| 女 |
|||
| 总计 |
30 |
并回答能否在犯错的概率不超过0.10的前提下认为性别与会围棋有关?
参考公式: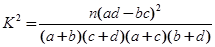 其中n=a+b+c+d
其中n=a+b+c+d
参考数据:
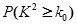 |
0.40 |
0.25 |
0.10 |
0.010 |
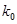 |
0.708 |
1.323 |
2.706 |
6.635 |
(Ⅱ)若从会围棋的选手中随机抽取3人成立该班围棋代表队,则该代表队中既有男又
有女的概率是多少?
(Ⅲ)若从14名女棋手中随机抽取2人参加棋类比赛,记会围棋的人数为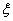 ,求
,求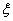 的期望.
的期望.