(本小题满分12分)为了响应国家号召,某地决定分批建设保障性住房供给社会.首批计划用100万元购得一块土地,该土地可以建造每层1 000平方米的楼房,楼房的每平方米建筑费用与建筑高度有关,楼房每升高一层,整层楼每平方米建筑费用提高20元.已知建筑第5层楼房时,每平方米建筑费用为800元.
(1)若建筑第x层楼时,该楼房综合费用为y万元(综合费用是建筑费用与购地费用之和),写出y=f(x)的表达式;
(2)为了使该楼房每平方米的平均综合费用最低,应把楼层建成几层?此时平均综合费用为每平方米多少元?
已知过抛物线
的焦点,斜率为
的直线交抛物线于
两点,且
.
(1)求该抛物线的方程;
(2)
为坐标原点,
为抛物线上一点,若
,求
的值.
如图,在
中,
,
,
为
边上一动点,
交
于点
,现将
沿
翻折至
,使平面
.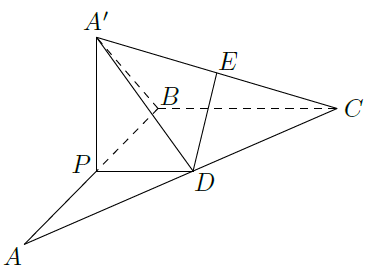
(1)当棱锥
的体积最大时,求
的长;
(2)若点
为
的中点,E为
的中点,求证:
.
在
中,
的对边分别是
,已知
.
(1)求
的值;
(2)若
,求边
的值.
某饮料公司对一名员工进行测试以便确定其考评级别.公司准备了两种不同的饮料共
杯,其颜色完全相同,并且其中
杯为
饮料,另外
杯为
饮料,公司要求此员工一一品尝后,从
杯饮料中选出
杯
饮料.若该员工
杯都选对,则评为优秀;若3杯选对
杯,则评为良好;否则评为及格.假设此人对A和B两种饮料没有鉴别能力.
(1)求此人被评为优秀的概率;
(2)求此人被评为良好及以上的概率.
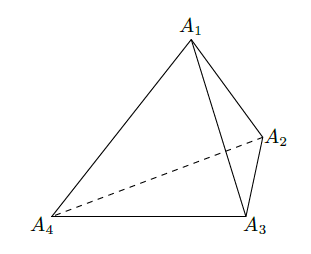
(1)如图,对于任一给定的四面体
,找出依次排列的四个相互平行的平面
,使得
(
=1,2,3,4),且其中每相邻两个平面间的距离都相等;
(2)给定依次排列的四个相互平行的平面
,其中每相邻两个平面间的距离为1,若一个正四面体
的四个顶点满足:
(
=1,2,3,4),求该正四面体
的体积.