如图,⊙O的弦AB=8,直径CD⊥AB于M,OM:MD=3:2,E是劣弧CB上一点,连结CE并延长交CE的延长线于点F.求: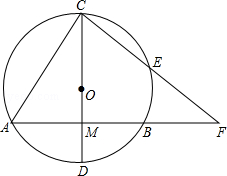
(1)⊙O的半径;
(2)求CE•CF的值.
(本题10分)已知:抛物线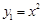 以点C为顶点且过点B,抛物线
以点C为顶点且过点B,抛物线 以点B为顶点且过点C,分别过点B、C作
以点B为顶点且过点C,分别过点B、C作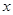 轴的平行线,交抛物线
轴的平行线,交抛物线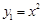 、
、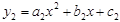 于点A、D,E、F分别为AB、CD中点,连结EC、BF,且AE=BF.
于点A、D,E、F分别为AB、CD中点,连结EC、BF,且AE=BF.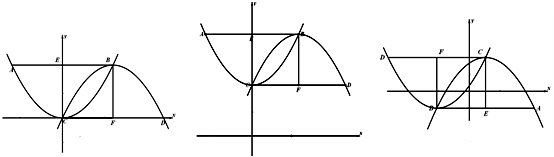
(1)如图1,①求证四边形ECFB为正方形;②求点A的坐标;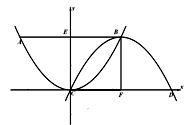
(2)①如图2,若将抛物线“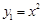 ”改为“
”改为“ ”,其他条件不变,求CD的长;
”,其他条件不变,求CD的长;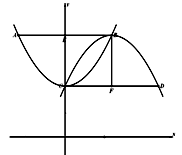
②如图3,若将抛物线“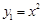 ”改为“
”改为“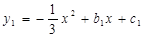 ”,其他条件不变,求
”,其他条件不变,求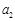 的值;
的值;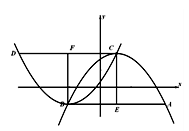
(3)若将抛物线“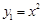 ”改为抛物线“
”改为抛物线“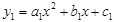 ”,其他条件不变,请用含b2的
”,其他条件不变,请用含b2的
代数式表示b1.
(本题10分)如图,在锐角△ABC中,AB>AC,AD⊥BC于D,以AD为直径的⊙O分别交AB,AC于E,F,连结DE,DF.
(1)已知P是射线DC上一个动点,当点P运动到PD=BD时,连结AP,交⊙O于G,连结DG.求证:∠EDG+∠BAC=180°;
(2)若∠BAC=70°,∠APB=50°,⊙O 的半径长为1,①求∠EDF的度数;②求劣弧DF的长.
(本题8分)如图,四边形ABCD是正方形,BE⊥BF,BE=BF,EF与BC交于点G.
(1)求证: ;
;
(2)若 求
求 的大小.
的大小.
(本题8分)2012年5月13日是母亲节,某校开展了形式多样的感恩教育活动.该校从每班随机抽取一部分学生进行调查,并将调查结果绘制成如下的扇形统计图和频数分布直方图.
根据上图信息,解答下列问题:
(1)求出本次被调查的学生人数,并补全频数分布直方图;
(2)若这所学校共有学生2400人,已知被调查的学生中,知道母亲生日的女生人数是男生人数的2倍,请根据上述调查结果估计该校知道母亲生日的女生有多少人?
(本题6分)解不等式组 .
.