(本小题满分10分)选修4-4:坐标系与参数方程
已知在平面直角坐标系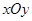 中,直线
中,直线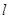 的参数方程是
的参数方程是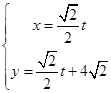 (t是参数),以原点O为极点,x轴正半轴建立极坐标系,曲线C的极坐标方程
(t是参数),以原点O为极点,x轴正半轴建立极坐标系,曲线C的极坐标方程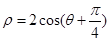 .
.
(Ⅰ)判断直线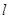 与曲线C的位置关系;
与曲线C的位置关系;
(Ⅱ)设M为曲线C上任意一点,求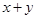 的取值范围.
的取值范围.
(本小题满分12分) 直角坐标系xOy中,以原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的方程为
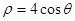 ,直线
,直线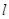 方程为
方程为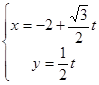 (t为参数),直线
(t为参数),直线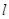 与C的公共点为T.
与C的公共点为T.
(1)求点T的极坐标;
(2)过点T作直线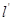 ,
,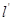 被曲线C截得的线段长为2,求直线
被曲线C截得的线段长为2,求直线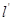 的极坐标方程.
的极坐标方程.
在极坐标系中,动点P(ρ,θ)运动时,ρ与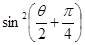 成反比,动点P的轨迹经过点(2,0).
成反比,动点P的轨迹经过点(2,0).
(1)求动点P的轨迹的极坐标方程;
(2)将(1)中极坐标方程化为直角坐标方程,并指出轨迹是何种曲线.
设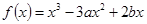 在x=1处有极小值-1,
在x=1处有极小值-1,
(1)试求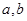 的值; (2)求出
的值; (2)求出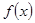 的单调区间.
的单调区间.
设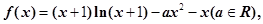
(1)若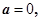 求函数
求函数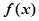 的极值点及相应的极值;
的极值点及相应的极值;
(2)若对任意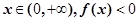 恒成立,求实数
恒成立,求实数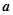 的取值范围.
的取值范围.
由下列各个不等式: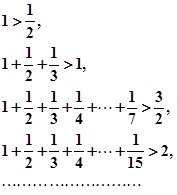
你能得到一个怎样的一般不等式?并加以证明.