先化简,再求值: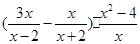 ,再选择一个使原式有意义的x代入求值.
,再选择一个使原式有意义的x代入求值.
如图,在平面直角坐标系中,四边形OABC是矩形,点B的坐标为(4,3).平行于对角线AC的直线m从原点O出发,沿x轴正方向以每秒1个单位长度的速度运动,设直线m与矩形OABC的两边分别交于点M、N,直线m运动的时间为t(秒).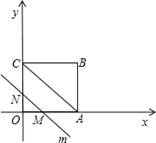
(1)点A的坐标是 ,点C的坐标是 ;
(2)当t= 秒或 秒时,MN=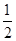 AC;
AC;
(3)设△OMN的面积为S,求S与t的函数关系式.
已知:如图,在矩形ABCD中,M,N分别是边AD,BC的中点,E,F分别是线段BM,CM的中点.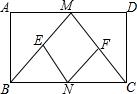
(1)求证:△ABM≌△DCM;
(2)判断四边形MENF是什么特殊四边形,并证明你的结论;
(3)当AD:AB= 时,四边形MENF是正方形(只写结论,不需证明).
如图,抛物线y=ax2+bx(a>0)经过原点O和点A(2,0).
(1)写出抛物线的对称轴与x轴的交点坐标;
(2)点(x1,y1),(x2,y2)在抛物线上,若x1<x2<1,比较y1,y2的大小;
(3)点B(-1,2)在该抛物线上,点C与点B关于抛物线的对称轴对称,求直线AC的函数关系式.
李老师为了了解所教班级学生完成数学课前预习的具体情况,对本班部分学生进行了为期半个月的跟踪调查,他将调查结果分为四类,A:很好;B:较好;C:一般;D:较差.并将调查结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题: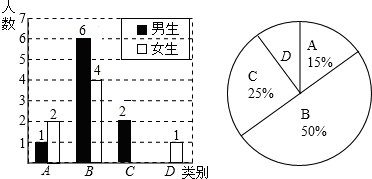
(1)李老师一共调查了多少名同学?
(2)C类女生有 名,D类男生有 名,将图1条形统计图补充完整;
(3)为了共同进步,李老师想从被调查的A类和D类学生中各随机选取一位同学进行“一帮一”互助学习,请用列表法或画树形图的方法求出所选两位同学恰好是一位男同学和一位女同学的概率.