(本小题满分10分)已知函数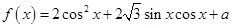 ,且当
,且当 时,
时,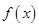 的最小值为2,
的最小值为2,
(1)求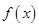 的单调递增区间;
的单调递增区间;
(2)先将函数 的图象上的点纵坐标不变,横坐标缩小到原来的
的图象上的点纵坐标不变,横坐标缩小到原来的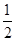 ,再把所得的图象向右平移
,再把所得的图象向右平移 个单位,得到函数
个单位,得到函数 的图象,求方程
的图象,求方程 在区间
在区间 上所有根之和.
上所有根之和.
已知抛物线
 的焦点为
的焦点为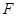 ,抛物线上存在一点
,抛物线上存在一点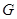 到焦点的距离为
到焦点的距离为 ,且点
,且点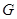 在圆
在圆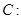
 上.
上.
(Ⅰ)求抛物线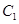 的方程;
的方程;
(Ⅱ)已知椭圆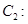
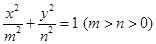 的一个焦点与抛物线
的一个焦点与抛物线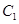 的焦点重合,且离心率为
的焦点重合,且离心率为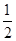 .直线
.直线 交椭圆
交椭圆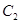 于
于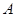 、
、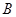 两个不同的点,若原点
两个不同的点,若原点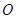 在以线段
在以线段 为直径的圆的外部,求
为直径的圆的外部,求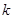 的取值范围.
的取值范围.
如图,在正四棱台 中,
中, ,
,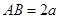 ,
, ,
, 、
、 分别是
分别是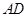 、
、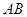 的中点.
的中点. 
(Ⅰ)求证:平面 ∥平面
∥平面 ;
;
(Ⅱ)求证: 平面
平面 .
.
注:底面为正方形,从顶点向底面作垂线,垂足是底面中心,这样的四棱锥叫做正四棱锥.用一个平行于正四棱锥底面的平面去截该棱锥,底面与截面之间的部分叫做正四棱台.
已知向量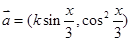 ,
,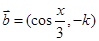 ,实数
,实数 为大于零的常数,函数
为大于零的常数,函数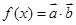 ,
, ,且函数
,且函数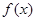 的最大值为
的最大值为 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)在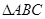 中,
中, 分别为内角
分别为内角 所对的边,若
所对的边,若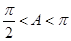 ,
, ,且
,且 ,
, ,求
,求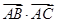 的值.
的值.
某区工商局、消费者协会在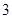 月
月 号举行了以“携手共治,畅享消费”为主题的大型宣传咨询服务活动,着力提升消费者维权意识.组织方从参加活动的群众中随机抽取
号举行了以“携手共治,畅享消费”为主题的大型宣传咨询服务活动,着力提升消费者维权意识.组织方从参加活动的群众中随机抽取 名群众,按他们的年龄分组:第
名群众,按他们的年龄分组:第 组
组 ,第
,第 组
组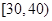 ,第
,第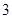 组
组 ,第
,第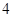 组
组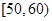 ,第
,第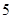 组
组 ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.
(Ⅰ)若电视台记者要从抽取的群众中选 人进行采访,求被采访人恰好在第
人进行采访,求被采访人恰好在第 组或第
组或第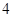 组的概率;
组的概率;
(Ⅱ)已知第 组群众中男性有
组群众中男性有 人,组织方要从第
人,组织方要从第 组中随机抽取
组中随机抽取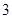 名群众组成维权志愿者服务队,求至少有两名女性的概率.
名群众组成维权志愿者服务队,求至少有两名女性的概率.
已知函数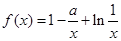 (
(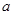 为实数).
为实数).
(Ⅰ)当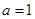 时,求函数
时,求函数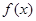 的图象在点
的图象在点 处的切线方程;
处的切线方程;
(Ⅱ)设函数 (其中
(其中 为常数),若函数
为常数),若函数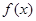 在区间
在区间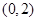 上不存在极值,且存在
上不存在极值,且存在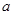 满足
满足
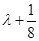 ,求
,求 的取值范围;
的取值范围;
(Ⅲ)已知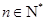 ,求证:
,求证: .
.