甲、乙两支球队进行总决赛,比赛采用七场四胜制,即若有一队先胜四场,则此队为总冠军,比赛就此结束.因两队实力相当,每场比赛两队获胜的可能性均为二分之一.据以往资料统计,第一场比赛可获得门票收入 万元,以后每场比赛门票收入比上一场增加
万元,以后每场比赛门票收入比上一场增加 万元.
万元.
(Ⅰ)求总决赛中获得门票总收入恰好为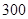 万元的概率;
万元的概率;
(Ⅱ)设总决赛中获得的门票总收入为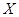 ,求
,求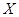 的分布列.
的分布列.
直三棱柱 中,
中, ,
, 分别是
分别是 的中点,
的中点, ,
, 为棱
为棱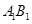 上的点.
上的点.
(1)证明: ;
;
(2)是否存在一点 ,使得平面
,使得平面 与平面
与平面 所成锐二面角的余弦值为
所成锐二面角的余弦值为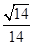 ?若存在,说明点
?若存在,说明点 的位置,若不存在,说明理由.
的位置,若不存在,说明理由.
设数列 的前
的前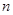 项和为
项和为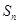 ,已知
,已知 ,且
,且 成等比数列,
成等比数列,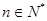 .
.
(1)求数列 的通项公式;
的通项公式;
(2)设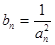 ,数列
,数列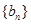 前
前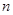 项和为
项和为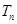 ,求证
,求证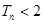 .
.
某商店计划每天购进某商品若干件,商店每销售一件该商品可获利润50元.供大于求时,剩余商品全部退回,但每件商品亏损10元;若供不应求,则从外部调剂,此时每件调剂商品可获利30元.
(1)若商店一天购进该商品10件,求当天的利润 (单位:元)关于当天需求量
(单位:元)关于当天需求量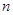 (单位:件,
(单位:件,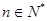 )的函数解析式;
)的函数解析式;
(2)商店记录了50天该商品的日需求量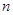 (单位:件),整理得下表:
(单位:件),整理得下表:
若商店一天购进10件该商品,以50天记录的各需求量的频率作为各需求量发生的概率,求该商品一天的利润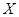 的分布列及平均值.
的分布列及平均值.
设 的内角
的内角 的对边分别为
的对边分别为 ,若
,若 ,且
,且 ,求
,求 及
及 的面积.
的面积.
设关于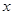 的函数
的函数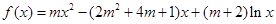 ,其中
,其中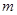 为实数集R上的常数,函数
为实数集R上的常数,函数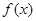 在
在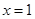 处取得极值0.
处取得极值0.
(1)已知函数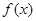 的图象与直线
的图象与直线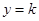 有两个不同的公共点,求实数k的取值范围;
有两个不同的公共点,求实数k的取值范围;
(2)设函数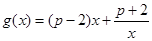 , 其中
, 其中 ,若对任意的
,若对任意的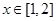 ,总有
,总有 成立,求
成立,求 的取值范围.
的取值范围.