(.天津市,第21题,10分)(本小题10分)
已知A, B,C是⊙O上的三个点,四边形OABC是平行四边形,过点C作⊙O的切线,交AB的延长线于点D.
(Ⅰ)如图①,求∠ADC的大小;
(Ⅱ)如图②,经过点O作CD的平行线,与AB交于点E,与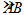 交于点F,连接AF,求∠FAB的大小.
交于点F,连接AF,求∠FAB的大小.
已知: 是等腰三角形, , .点 在边 上,点 在边 上(点 、点 不与所在线段端点重合), ,连接 , ,射线 ,延长 交射线 于点 ,点 在直线 上,且 .
(1)如图,当 时
①求证: ;
②求 的度数;
(2)当 ,其它条件不变时, 的度数是 ;(用含 的代数式表示)
(3)若 是等边三角形, ,点 是 边上的三等分点,直线 与直线 交于点 ,请直接写出线段 的长.

如图,在平面直角坐标系中,点 的坐标为 .点 的坐标为 ,直线 经过点 和点 ,直线 与直线 相交于点 .
(1)求直线 的表达式和点 的坐标;
(2)矩形 的边 在 轴的正半轴上,点 与点 重合,点 在线段 上,边 平行于 轴,且 , ,将矩形 沿射线 的方向平移,边 始终与 轴平行.已知矩形 以每秒 个单位的速度匀速移动(点 移动到点 时停止移动),设移动时间为 秒 .
①矩形 在移动过程中, 、 、 三点中有且只有一个顶点落在直线 或 上,请直接写出此时 的值;
②若矩形 在移动的过程中,直线 交直线 于点 ,交直线 于点 .当 的面积等于18时,请直接写出此时 的值.

如图, 是 的直径,点 和点 是 上的两点,过点 作 的切线交 延长线于点 .
(1)若 ,求 的度数;
(2)若 , ,求 半径的长.

某公司今年1月份的生产成本是400万元,由于改进技术,生产成本逐月下降,3月份的生产成本是361万元.
假设该公司2、3、4月每个月生产成本的下降率都相同.
(1)求每个月生产成本的下降率;
(2)请你预测4月份该公司的生产成本.
九年三班的小雨同学想了解本校九年级学生对哪门课程感兴趣,随机抽取了部分九年级学生进行调查(每名学生必选且只能选择一门课程).将获得的数据整理绘制如下两幅不完整的统计图.

根据统计图提供的信息,解答下列问题:
(1)在这次调查中一共抽取了 名学生, 的值是 .
(2)请根据以上信息直接在答题卡上补全条形统计图;
(3)扇形统计图中,“数学”所对应的圆心角度数是 度;
(4)若该校九年级共有1000名学生,根据抽样调查的结果,请你估计该校九年级学生中有多少名学生对数学感兴趣.