已知: 是等腰三角形, , .点 在边 上,点 在边 上(点 、点 不与所在线段端点重合), ,连接 , ,射线 ,延长 交射线 于点 ,点 在直线 上,且 .
(1)如图,当 时
①求证: ;
②求 的度数;
(2)当 ,其它条件不变时, 的度数是 ;(用含 的代数式表示)
(3)若 是等边三角形, ,点 是 边上的三等分点,直线 与直线 交于点 ,请直接写出线段 的长.

实施乡村振兴计划以来,我市农村经济发展进入了快车道,为了解梁家岭村今年一季度经济发展状况,小玉同学的课题研究小组从该村300户家庭中随机抽取了20户,收集到他们一季度家庭人均收入的数据如下(单位:万元)
0.69 0.73 0.74 0.80 0.81 0.98 0.93 0.81 0.89 0.69
0.74 0.99 0.98 0.78 0.80 0.89 0.83 0.89 0.94 0.89
研究小组的同学对以上数据进行了整理分析,得到下表:
|
分组 |
频数 |
|
|
2 |
|
|
3 |
|
|
1 |
|
|
|
|
|
4 |
|
|
2 |
|
|
|
|
统计量 |
平均数 |
中位数 |
众数 |
|
数值 |
0.84 |
|
|
(1)表格中: , , , ;
(2)试估计今年一季度梁家岭村家庭人均收入不低于0.8万元的户数;
(3)该村梁飞家今年一季度人均收入为0.83万元,能否超过村里一半以上的家庭?请说明理由.
如图,抛物线 与 轴交于点 , ,与 轴交于点 ,已知 , 两点坐标分别是 , ,连接 , .
(1)求抛物线的表达式和 所在直线的表达式;
(2)将 沿 所在直线折叠,得到 ,点 的对应点 是否落在抛物线的对称轴上,若点 在对称轴上,请求出点 的坐标;若点 不在对称轴上,请说明理由;
(3)若点 是抛物线位于第三象限图象上的一动点,连接 交 于点 ,连接 , 的面积记为 , 的面积记为 ,求 的值最大时点 的坐标.

如图,在 中, , 是 的外接圆, 是直径,交 于点 ,点 在 上,连接 , 过点 作 交 的延长线于点 ,延长 交 于点 .
(1)求证: 是 的切线;
(2)若 , ,求 和 的长.

如图,过 点的直线 与 轴, 轴分别交于点 , 两点,且 ,过点 作 轴,垂足为点 ,交反比例函数 的图象于点 ,连接 , 的面积为6.
(1)求 值和点 的坐标;
(2)如图,连接 , ,点 在直线 上,且位于第二象限内,若 的面积是 面积的2倍,求点 的坐标.

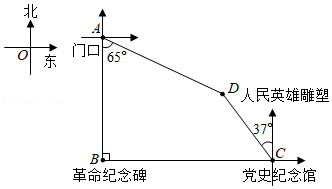
时代中学组织学生进行红色研学活动.学生到达爱国主义教育基地后,先从基地门口 处向正南方向走300米到达革命纪念碑 处,再从 处向正东方向走到党史纪念馆 处,然后从 处向北偏西 方向走200米到达人民英雄雕塑 处,最后从 处回到 处.已知人民英雄雕塑在基地门口的南偏东 方向,求革命纪念碑与党史纪念馆之间的距离(精确到1米).(参考数据: , , , , ,