(.河北省,第26题,14分) (本小题满分14分)
平面上,矩形ABCD与直径为QP的半圆K如图摆放,分别延长DA和QP交于点O,且∠BOQ=60°,OQ=OD=3,OP=2,OA=AB=1.让线段OD及矩形ABCD位置固定,将线段OQ连带着半圆K一起绕着点O按逆时针方向形如旋转,设旋转角为α(0°≤α≤60°).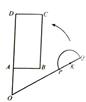
发现(1)当α=0°,即初始位置时,点P____直线AB上.(填“在”或“不在”)
求当α是多少时,OQ经过点B?
(2)在OQ旋转过程中.简要说明α是多少时,点P,A间的距离最小?并指出这个最小值:
(3)如图,当点P恰好落在BC边上时.求α及S阴影.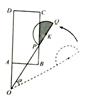
拓展如图.当线段OQ与CB边交于点M,与BA边交于点N时,设BM=x(x>0),用含x的代数式表示BN的长,并求x的取值范围.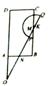
探究当半圆K与矩形ABCD的边相切时,求sin α的值.
已知:在△ABC中,∠BAC=90°,AB=AC,AE是过点A的一条直线,且BD⊥AE于D,CE⊥AE于E.
(1)当直线AE处于如图①的位置时,有BD=DE+CE,请说明理由;
(2)当直线AE处于如图②的位置时,则BD、DE、CE的关系如何?请说明理由;
(3)归纳(1)、(2),请用简洁的语言表达BD、DE、CE之间的关系.
智能手机如果安装了一款测量软件“Smart Measure”后,就可以测量物高、宽度和面积等.如图,打开软件后将手机摄像头的屏幕准星对准脚部按键,再对准头部按键,即可测量出人体的高度.其数学原理如图②所示,测量者AB与被测量者CD都垂直于地面BC.
(1)若手机显示AC=1m,AD=1.8m,∠CAD=60°,求此时CD的高.(结果保留根号)
(2)对于一般情况,试探索手机设定的测量高度的公式:设AC=a,AD=b,∠CAD= ,即用a、b、
,即用a、b、 来表示CD.(提示:sin2
来表示CD.(提示:sin2 +cos2
+cos2 =1)
=1)
“五一”假期,某公司组织部分员工分别到甲、乙、丙、丁四地考察,公司按定额购买了前往各地的车票,如图所示是用来制作完整的车票种类和相应数量的条形统计图,根据统计图回答下列问题:
(1)若去丁地的车票占全部车票的10%,请求出去丁地的车票数量,并补全统计图(如图所示).
(2)若公司采用随机抽取的方式发车票,小胡先从所有的车票中随机抽取一张(所有车票的形状、大小、质地完全相同、均匀),那么员工小胡抽到去甲地的车票的概率是多少?
(3)若有一张车票,小王和小李都想去,决定采取摸球的方式确定,具体规则:“每人从不透明袋子中摸出分别标有1、2、3、4的四个球中摸出一球(球除数字不同外完全相同),并放回让另一人摸,若小王摸得的数字比小李的小,车票给小王,否则给小李.”试用列表法或画树状图的方法分析这个规则对双方是否公平?
如图,已知E是平行四边形ABCD对角线AC上的点,连接DE.
(1)过点B在平行四边形内部作射线BF交AC于点F,且使∠CBF=∠ADE(要求:用尺规作图,保留作图痕迹,不写作法与证明)
(2)连接BE,DF,判断四边形BFDE的形状并证明.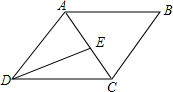
如图,在△ABC中,AB=AC,D是BA延长线上的一点,点E是AC的中点.
(1)实践与操作:利用尺规按下列要求作图,并在图中标明相应字母(保留作图痕迹,不写作法).
①作∠DAC的平分线AM. ②连接BE并延长交AM于点F.
(2)猜想与证明:试猜想AF与BC有怎样的位置关系和数量关系,并说明理由.