（.宁夏，第26题，10分）如图，是一副学生用的三角板，在△ABC 中，∠C=90°, ∠A=60°，∠B=30°；在△
中，∠C
=90°, ∠A=45°，∠B=45°，且AB=" CB" ．若将边
与边CA重合，其中点
与点C重合．将三角板绕点C（）按逆时针方向旋转，旋转过的角为
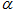，旋转过程中边与边AB的交点为M, 设AC=
．
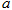（1）计算的长；
（2）当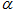=30°时，证明：
∥AB；
（3）若=
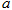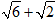，当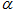=45°时，计算两个三角板重叠部分图形的面积；
（4）当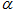=60°时，用含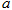的代数式表示两个三角板重叠部分图形的面积．
（参考数据：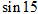
°= 
，
°= 
，
°=
°= , 
°= , 
°=
）
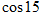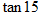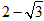
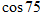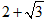某水渠的横截面呈抛物线形，水面的宽为AB(单位：米)。现以AB所在直线为x轴．以抛物线的对称轴为y轴建立如图所示的平面直角坐标系,设坐标原点为O．已知AB=8米。设抛物线解析式为
．
（1）求a的值；
（2）点C(一1，m)是抛物线上一点，点C关于原点D的对称点为点D，连接CD、BC、BD，求△BCD的面积．
春雷中学要了解全校学生对不同类别电视节目的喜爱情况，围绕“在体育、新闻、动画、娱乐四类电视节目中，你最喜欢哪一类?(必选且只选一类)”的问题，在全校范围内随机抽取部分学生进行问卷调查．将调查结果整理后绘制成如图所示的不完整的条形统计图．其中最喜欢新闻类电视节目的人数占被抽取人数的l0％．请你根据以上信息回答下列问题：
（1）在这次调查中，最喜欢新闻类电视节目的学生有多少名?并补全条形统计图：
（2）如果全校共有l 200名学生，请你估计全校学生中最喜欢体育类电视节目的学生有多少名?
如图。在每个小正方形的边长均为1个单位长度的方格纸中,有线段
和直线
，点
均在小正方形的顶点上．
（1）在方格纸中画四边形
(四边形的各顶点均在小正方形的顶点上)，使四边形
是以直线
为对称轴的轴对称图形，点
的对称点为点
，点
的对称点为点
；
（2）请直接写出四边形
的周长．
先化简，再求代数式
的值，其中
如图，抛物线
与直线
交于C，D两点，其中点C在y轴上，点D的坐标为
。点P是y轴右侧的抛物线上一动点，过点P作PE⊥x轴于点E，交CD于点F.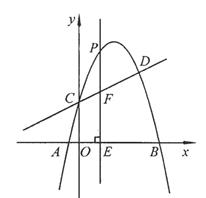
（1）求抛物线的解析式；
（2）若点P的横坐标为m，当m为何值时，以O，C，P，F为顶点的四边形是平行四边形？请说明理由；
（3）若存在点P，使∠PCF=450，请直接写出相应的点P的坐标。