(本小题满分14分)设全集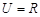 ,函数
,函数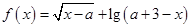 的定义域为集合
的定义域为集合 ,集合
,集合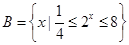 .
.
(1)若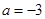 ,求
,求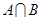 ,
,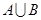 ;
;
(2)若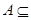 C UB,求实数
C UB,求实数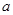 的取值范围.
的取值范围.
(本小题满分16分)
已知△ABC中,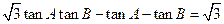 .
.
(I)求∠C的大小;
(Ⅱ)设角A,B,C的对边依次为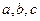 ,若
,若 ,且△ABC是锐角三角形,求
,且△ABC是锐角三角形,求 的取值范围.
的取值范围.
(本小题满分15分)
运货卡车以每小时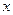 千米的速度匀速行驶130千米
千米的速度匀速行驶130千米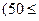
 (单位:千米/小时).假设汽油的价格是每升2元,而汽车每小时耗油
(单位:千米/小时).假设汽油的价格是每升2元,而汽车每小时耗油 升,司机的工资是每小时14元.
升,司机的工资是每小时14元.
(1)求这次行车总费用 关于
关于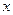 的表达式;
的表达式;
(2)当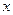 为何值时,这次行车的总费用最低,并求出最低费用的值.
为何值时,这次行车的总费用最低,并求出最低费用的值.
(本小题满分15分)

数列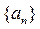 中,
中, ,
, ,
,
(1)若数列 为公差为11的等差数列,求
为公差为11的等差数列,求 ;
;
(2)若数列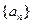 为以
为以 为首项的等比数列,求数列
为首项的等比数列,求数列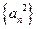 的前m项和
的前m项和
(本小题满分14分)


如图,在正方体ABCD-A1B1C1D1中,E、F为棱AD、AB的中点.
(1)求证:EF∥平面CB1D1;
(2)求证:平面CAA1C1⊥平面CB1D1.
(本小题满分14分)

已知函数
(Ⅰ)求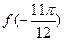 的值;
的值;
(Ⅱ)当 时,求
时,求 的最大值和最小值.
的最大值和最小值.