(本小题满分12分)《中华人民共和国个人所得税》规定,公民全月工资、薪金所得不超过2000元的部分不必纳税,超过2000元的部分为全月应纳税所得额,此项税款按下表分段累计计算:
| 全月应纳税所得额 |
税率(%) |
| 不超过500元的部分 |
5 |
| 超过500元至2000元的部分 |
10 |
| 超过2000元至5000元的部分 |
15 |
(1)设当月应激纳此项税款为 元,当月工资、薪金所得为
元,当月工资、薪金所得为 元,把
元,把 表示成
表示成 的函数;
的函数;
(2)某人一月份应激纳此项税款为26.78元,那么他当月的工资、薪金所得是多少?
(本小题满分12分)现要围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需要维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,如图所示,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为x(单位:米),修建此矩形场地围墙的总费用为y(单位:元)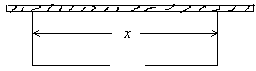
(1)将y表示为x的函数;
(2)试确定x,使修建此矩形场地围墙的总费用最小,并求出最小总费用。
(本小题满分12分)已知函数 .
.
(1)求函数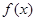 的最小正周期和最大值;(2)求
的最小正周期和最大值;(2)求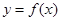 在R上的单调区间.
在R上的单调区间.
(本小题满分12分)已知函数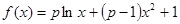 .
.
(1)讨论函数 的单调性;
的单调性;
(2)当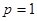 时,
时,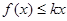 恒成立,求实数
恒成立,求实数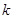 的取值范围;
的取值范围;
(3)证明: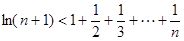
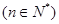 .
.
(本小题满分12分)
已知点 是椭圆
是椭圆 的右焦点,点
的右焦点,点 、
、 分别是
分别是 轴、
轴、 轴上的动点,且满足
轴上的动点,且满足 .若点
.若点 满足
满足 .
.
(1)求点 的轨迹
的轨迹 的方程;
的方程;
(2)设过点 任作一直线与点
任作一直线与点 的轨迹交于
的轨迹交于 、
、 两点,直线
两点,直线 、
、 与直线
与直线 分别交于点
分别交于点 、
、 (
( 为坐标原点),试判断
为坐标原点),试判断 是否为定值?若是,求出这个定值;若不是,请说明理由.
是否为定值?若是,求出这个定值;若不是,请说明理由.
如图,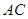 是圆
是圆 的直径,点
的直径,点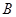 在圆
在圆 上,
上, ,
,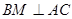 交
交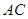 于点
于点 ,
,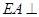 平面
平面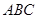 ,
, ,
,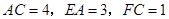 .
.
(1)证明: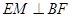 ;
;
(2)求平面 与平面
与平面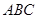 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.