抛物线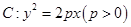 的准线
的准线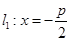 过双曲线
过双曲线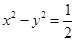 的一个焦点.
的一个焦点.
(1)求抛物线C的方程;
(2)设M为抛物线C上任意一点.
①设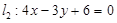 ,求
,求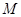 到
到 与
与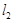 距离之和的最小值;
距离之和的最小值;
②以M为切点的抛物线的切线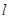 与
与 交于点N,试问
交于点N,试问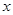 轴上是否存在定点Q,使Q在以MN为直径的
轴上是否存在定点Q,使Q在以MN为直径的
圆上.若存在,求出点Q坐标,若不存在,说明理由.
已知△ABC的三个内角A、B、C所对的边分别为a,b, c,向量m=(1,1- sinA),n=(cosA,1),且m⊥n.
sinA),n=(cosA,1),且m⊥n.
(Ⅰ)求角A;
(Ⅱ)若b+c= a,求sin(B+
a,求sin(B+ )的值.
)的值.
已知集合U={x|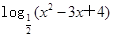 >-2且x∈Z},集合A={x|ax-1=0},集合B={x|
>-2且x∈Z},集合A={x|ax-1=0},集合B={x|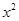 -(a+3)x+2a+2=0),若CUA=B,求a的值.
-(a+3)x+2a+2=0),若CUA=B,求a的值.
已知中心在原点,焦点在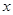 轴上的椭圆,离心率
轴上的椭圆,离心率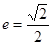 ,且经过抛物线
,且经过抛物线 的焦点.
的焦点.
(1)求椭圆的标准方程;
(2)若过点 的直线
的直线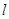 (斜率不等于零)与椭圆交于不同的两点
(斜率不等于零)与椭圆交于不同的两点 (
( 在
在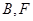
之间), 与
与 面积之比为
面积之比为 ,求
,求 的取值范围.
的取值范围.
已知函数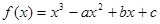 的图象为曲线C。
的图象为曲线C。
(1)若曲线C上存在点P,使曲线C在P点处的切线与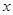 轴平行,求
轴平行,求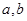 的关系;
的关系;
(2)若函数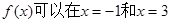 时取得极值,求此时
时取得极值,求此时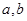 的值;
的值;
(3)在满足(2)的条件下,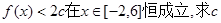 的取值范围。
的取值范围。
已知数列 是首项为
是首项为 ,公比
,公比 的等比数列,设
的等比数列,设 ,数列
,数列 .
.
(1)求数列 的通项公式;(2)求数列
的通项公式;(2)求数列 的前n项和Sn.
的前n项和Sn.