已知点A在数轴上对应的数为a，点B对应的数为b，且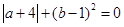
，A、B之间的距离记作|AB|，
（1）求线段AB的长|AB|；
（2）设点P在数轴上对应的数为x，当|PA|－|PB|＝2时，求x的值；
（3）若点P在点A的左侧，M、N分别是PA、PB的中点，当点P在A的左侧移动时，下列两个结论：①|PM|＋|PN|的值不变；②|PN|－|PM|的值不变，其中只有一个结论正确，请判断出正确结论，并求其值．
解方程
（1）4x2－3x＋2＝0
（2）
如图，有一边长为5的正方形ABCD和等腰△PQR，PQ=PR=5cm，QR=8cm，点B，C，Q，R在同一条直线m上，当C，Q两点重合时，等腰△PQR以每秒1cm的速度沿直线m按箭头所示的方向开始匀速运动，t秒后正方形ABCD和等腰△PQR重合部分的面积为Scm2
（1） 当t =3秒时，设PQ与CD相交于点F，点E为QR的中点，连结PE求证：ΔQCF∽ΔQEP
（2）当t =6秒时，求S的值
（3）当8≤t≤13，求S关于t的函数解析式
已知反比例函数
和一次函数y=-x+a-1（a为常数）
（1）当a＝5时，求反比例函数与一次函数的交点坐标
（2）是否存在实数a，使反比例函数与一次函数有且只有一个交点，如果存在，求出实数a，如果不存在，说明理由
小明想利用太阳光测量楼高。他带着皮尺来到一栋楼下，发现对面墙上有这栋楼的影子，针对这种情况，他设计了一种测量方案，具体测量情况如下：如示意图，小明边移动边观察，发现站到点
处时，可以使自己落在墙上的影子与这栋楼落在墙上的影子重叠，且高度恰好相同．此时，测得小明落在墙上的影子高度CD＝1.2m，CE＝0.8m，CA＝30m（点A、E、C在同一直线上）．已知小明的身高EF是1.7m，请你帮小明求出楼高AB（结果精确到0.1m）．
如图，已知△ABC中CE⊥AB于E，BF⊥AC于F,
（1）求证：ΔABF ∽ΔACE
（2）求证：ΔAEF ∽ΔACB
（3）若∠A=60， 求：