(本小题满分12分)
随机调查某社区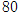 个人,以研究这一社区居民在20:00——22:00时间段的休闲方式与性别的关系,得到下面的数据表:
个人,以研究这一社区居民在20:00——22:00时间段的休闲方式与性别的关系,得到下面的数据表:
| 休闲方式 性别 |
看电视 |
看书 |
合计 |
| 男 |
 |
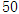 |
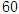 |
| 女 |
 |
 |
 |
| 合计 |
 |
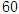 |
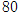 |
(1)从这80人中按照性别进行分层抽样,抽出4人,则男女应各抽取多少人;
(2)从第(1)问抽取的4位居民中随机抽取2位,恰有1男1女的概率是多少;
(3)由以上数据,能否有99%的把握认为在20:00—22:00时间段的休闲方式与性别有关系.
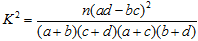 ,其中
,其中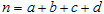 .
.
参考数据:
 |
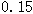 |
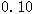 |
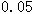 |
 |
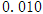 |
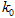 |
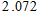 |
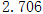 |
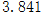 |
 |
 |
设函数 .
.
(1)求函数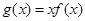 在区间
在区间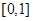 的最小值;
的最小值;
(2)当 时,记曲线
时,记曲线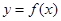 在
在 处的切线为
处的切线为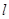 ,
,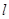 与
与 轴交于点
轴交于点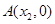 ,求证:
,求证: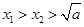 .
.
设数列 的前
的前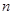 项和为
项和为 ,且满足
,且满足 ,
, ,
,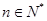 .
.
(1)猜想 的通项公式,并加以证明;
的通项公式,并加以证明;
(2)设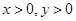 ,且
,且 ,证明:
,证明: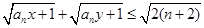 .
.
设函数 ,其中
,其中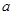 为大于零的常数.
为大于零的常数.
(1)当 时,求函数
时,求函数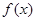 的单调区间和极值;
的单调区间和极值;
(2)若在区间 上至少存在一点
上至少存在一点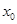 ,使得
,使得 成立,求
成立,求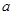 的取值范围.
的取值范围.
用0,1,2,3,4,5这六个数字组成无重复数字的五位数.试分别求出符合下列条件的五位数的个数(最后结果用数字表达):
(1)总的个数;
(2)奇数;
(3)能被6整除的数;
(4)比12345大且能被5整除的数.
已知 的展开式中,第
的展开式中,第 项的系数与第
项的系数与第 项的系数之比是10:1,求展开式中,
项的系数之比是10:1,求展开式中,
(1)含 的项;
的项;
(2)系数最大的项.