本题共有3个小题,第1小题4分,第2小题5分,第3小题5分.
设等比数列 的前
的前 项的和为
项的和为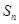 ,公比为
,公比为 .
.
(1)若 成等差数列,求证:
成等差数列,求证: 成等差数列;
成等差数列;
(2)若 (
(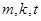 为互不相等的正整数)成等差数列,试问数列
为互不相等的正整数)成等差数列,试问数列 中是否存在不同的三项成等差数列?若存在,写出两组这三项;若不存在,请说明理由;
中是否存在不同的三项成等差数列?若存在,写出两组这三项;若不存在,请说明理由;
(3)若 为大于
为大于 的正整数.试问
的正整数.试问 中是否存在一项
中是否存在一项 ,使得
,使得 恰好可以表示为该数列中连续两项的和?请说明理由.
恰好可以表示为该数列中连续两项的和?请说明理由.
(本小题14分)已知中心在原点,焦点在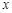 轴上的椭圆
轴上的椭圆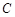 的离心率为
的离心率为 ,且经过点
,且经过点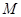
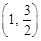 .
.
(Ⅰ)求椭圆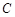 的方程;
的方程;
(Ⅱ)是否存过点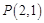 的直线
的直线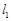 与椭圆
与椭圆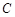 相交于不同的两点
相交于不同的两点 ,满足
,满足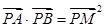 ?若存在,求出直线
?若存在,求出直线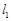 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
(本小题12分)已知函数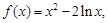

(Ⅰ)求函数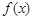 的极值;
的极值;
(Ⅱ)设函数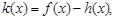 若函数
若函数 在
在 上恰有两个不同零点,求实数
上恰有两个不同零点,求实数 的取值范围.
的取值范围.
(本小题12分)设 .
.
(1)求函数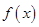 的单调区间;
的单调区间;
(2)若当 时
时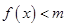 恒成立,求
恒成立,求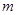 的取值范围
的取值范围
(本小题满分12分).设命题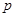 :“方程
:“方程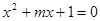 有两个实数根”;命题
有两个实数根”;命题 :“方程
:“方程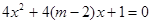 无实根”,若
无实根”,若 为假,
为假,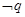 为假,求实数
为假,求实数 的取值范围.
的取值范围.
(本题15分)已知方程x2+y2-2(m+3)x+2(1-4m2)y+16m4+9=0表示一个圆
(1)求实数m的取值范围;
(2)求该圆半径r的取值范围;
(3)求圆心的轨迹方程。