(本小题满分10分)设命题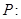 函数
函数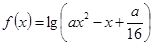 的定义域为
的定义域为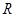 ;命题
;命题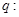 不等式
不等式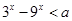 对一切正实数
对一切正实数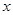 均成立..
均成立..
(1)如果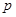 是真命题,求实数
是真命题,求实数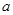 的取值范围;
的取值范围;
(2)如果命题“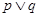 ”为真命题,且“
”为真命题,且“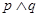 ”为假命题,求实数
”为假命题,求实数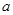 的取值范围.
的取值范围.
沪杭高速公路全长166千米,假设某汽车从上海莘庄镇进入该高速公路后以不低于60千米/时且不高于120千米/时的速度匀速行驶到杭州。已知该汽车每小时的运输成本(以元为单位)由可变部分和固定部分组成:可变部分与速度 (千米/时)的平方成正比,比例系数为0.02;固定部分为200元。
(千米/时)的平方成正比,比例系数为0.02;固定部分为200元。
(1)把全程运输成本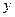 (元)表示为速度
(元)表示为速度 (千
(千 米/时)的函数,并指出这个函数的定义域;
米/时)的函数,并指出这个函数的定义域;
(2)汽车应以多大速度行驶才能使全程运输成本最小?最小运输成本为多少元?
已知函数
(1)求曲线 在点
在点 处的切线的方程;
处的切线的方程;
(2)直线 为曲线
为曲线 的切线,且经过原点,求直线
的切线,且经过原点,求直线 的方程及切点坐标。
的方程及切点坐标。
命题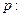 实数
实数 满足
满足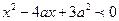 ,其中
,其中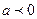 ;命题
;命题 实数
实数 满足
满足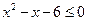 或
或 ,且
,且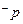 是
是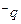 的必要不充分条件,求
的必要不充分条件,求 的取值范围
的取值范围
设 ,
, ,
,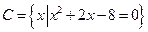 ,
, ,且
,且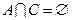 ,求
,求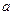 的值;
的值;
(本小题共12分)设x=3是函数f (x) = (x2+ax+b)·e3-x (x∈R)的一个极值点。
⑴求a与b的关系式,(用a表示b),并求f(x)的单调区间。
⑵设a>0, 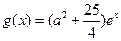 ,若存在ε1,ε2∈[0,4],使|f (ε1)-g (ε2)|<1成立,求a的取值范围。
,若存在ε1,ε2∈[0,4],使|f (ε1)-g (ε2)|<1成立,求a的取值范围。