某产品具有一定的时效性,在这个时效期内,由市场调查可知,在不做广告宣传且每件获利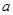 元的前提下,可卖出
元的前提下,可卖出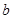 件;若做广告宣传,广告费为
件;若做广告宣传,广告费为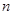 千元比广告费为
千元比广告费为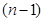 千元时多卖出
千元时多卖出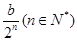 件.
件.
(Ⅰ)试写出销售量 与
与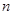 的函数关系式;
的函数关系式;
(Ⅱ)当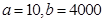 时,厂家应生产多少件这种产品,做几千元的广告,才能获利最大?
时,厂家应生产多少件这种产品,做几千元的广告,才能获利最大?
如图,四棱锥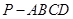 的底面
的底面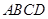 为矩形,且
为矩形,且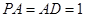 ,
, ,
,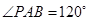 ,
,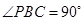 ,
,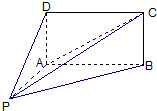
(Ⅰ)平面PAD与平面PAB是否垂直?并说明理由;
(Ⅱ)求直线PC与平面ABCD所成角的正弦值.
2013年4月14日,CCTV财经频道报道了某地建筑市场存在违规使用未经淡化海砂的现象.为了研究使用淡化海砂与混凝土耐久性是否达标有关,某大学实验室随机抽取了60个样本,得到了相关数据如下表:
| 混凝土耐久性达标 |
混凝土耐久性不达标 |
总计 |
|
| 使用淡化海砂 |
25 |
 |
30 |
| 使用未经淡化海砂 |
 |
15 |
30 |
| 总计 |
40 |
20 |
60 |
(Ⅰ)根据表中数据,求出 ,
, 的值,利用独立性检验的方法判断,能否在犯错误的概率不超过1%的前提下,认为使用淡化海砂与混凝土耐久性是否达标有关?
的值,利用独立性检验的方法判断,能否在犯错误的概率不超过1%的前提下,认为使用淡化海砂与混凝土耐久性是否达标有关?
(Ⅱ)若用分层抽样的方法在使用淡化海砂的样本中抽取了6个,现从这6个样本中任取2个,则取出的2个样本混凝土耐久性都达标的概率是多少?
参考数据:
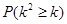 |
0.10 |
0.050 |
0.025 |
0.010 |
0.001 |
 |
2.706 |
3.841 |
5.024 |
6.635 |
10.828 |
参考公式: 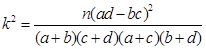
在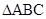 中,角
中,角 的对边分别为
的对边分别为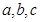 ,已知:
,已知: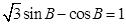 ,且
,且 .
.
(Ⅰ)若 ,求边
,求边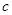 ;
;
(Ⅱ)若 ,求
,求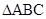 的面积.
的面积.
设函数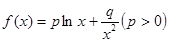 ,若
,若 时,
时, 有极小值
有极小值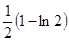 ,
,
(1)求实数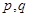 的取值;
的取值;
(2)若数列 中,
中,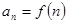 ,求证:数列
,求证:数列 的前
的前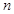 项和
项和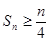 ;
;
(3)设函数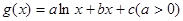 ,若
,若 有极值且极值为
有极值且极值为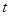 ,则
,则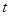 与
与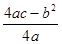 是否具有确定的大小关系?证明你的结论.
是否具有确定的大小关系?证明你的结论.