若 满足
满足 ,则称
,则称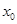 为
为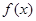 的不动点.
的不动点.
(1)若函数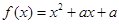 没有不动点,求实数
没有不动点,求实数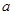 的取值范围;
的取值范围;
(2)若函数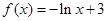 的不动点
的不动点 ,求
,求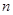 的值;
的值;
(3)若函数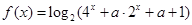 有不动点,求实数
有不动点,求实数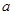 的取值范围.
的取值范围.
某公司“咨询热线”电话共有10路外线,经长期统计发现,在8点至10点这段时间内,英才苑外线电话同时打入情况如下表所示:
| 电话同时打入数ξ |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| 概率P |
0.13 |
0.35 |
0.27 |
0.14 |
0.08 |
0.02 |
0.01 |
0 |
0 |
0 |
0 |
(1)若这段时间内,公司只安排了2位接线员(一个接线员一次只能接一个电话).
①求至少一路电话不能一次接通的概率;
②在一周五个工作日中,如果有三个工作日的这一时间内至少一路电话不能一次接通,那么公司的形象将受到损害,现用至少一路电话一次不能接通的概率表示公司形象的“损害度”,求这种情况下公司形象的“损害度”;(2)求一周五个工作日的这一时间内,同时打入的电话数ξ的期望值.
(本题满分12分)已知向量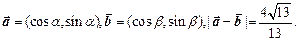
(1)求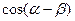 的值; (2)若
的值; (2)若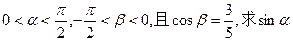 的值。
的值。
(本小题满分12分)
已知不等式 为大于2的整数,
为大于2的整数, 表示不超过
表示不超过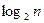 的最大整数. 设数列
的最大整数. 设数列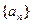 的各项为正,且满足
的各项为正,且满足
(Ⅰ)证明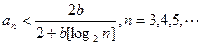
(Ⅱ)猜测数列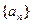 是否有极限?如果有,写出极限的值(不必证明);
是否有极限?如果有,写出极限的值(不必证明);
(Ⅲ)试确定一个正整数N,使得当 时,对任意b>0,都有
时,对任意b>0,都有 .
.
(本小题满分14分)
已知直线l与椭圆 (a>b>0)相交于不同两点A、B,
(a>b>0)相交于不同两点A、B, ,且
,且 ,以M为焦点,以椭圆的右准线为相应准线的双曲线与直线l相交于N(4,
,以M为焦点,以椭圆的右准线为相应准线的双曲线与直线l相交于N(4, 1). (I)求椭圆的离心率
1). (I)求椭圆的离心率 ; (II)设双曲线的离心率为
; (II)设双曲线的离心率为 ,记
,记 ,求
,求 的解析式,并求其定义域和值域.
的解析式,并求其定义域和值域.
(本小题满分12分)已知函数 ,
, .
.
(I)证明:当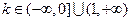 时,函数
时,函数 在其定义域内为单调函数;(II)若函数
在其定义域内为单调函数;(II)若函数 的图象在点(1,
的图象在点(1, )处的切线斜率为0,且当
)处的切线斜率为0,且当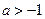 时,
时, ≥
≥ 在
在 上恒成立,求实数a的取值范围.
上恒成立,求实数a的取值范围.