浠水某商场要经营一种新上市的文具，进价为20元/件．试营销阶段发现：当销售单价是25元时，每天的销售量为250件；销售单价每上涨1元，每天的销售量就减少10件．
（1）写出商场销售这种文具，每天所得的销售利润w（元）与销售单价x（元）之间的函数关系式；
（2）求销售单价为多少元时，该文具每天的销售利润最大；
（3）商场的营销部结合上述情况，提出了A、B两种营销方案：
方案A：该文具的销售单价高于进价且不超过30元；
方案B：每天销售量不少于10件，且每件文具的利润至少为25元
请比较哪种方案的最大利润更高，并说明理由．
（年贵州省毕节）如图，抛物线y=x2+bx+c与x轴交于A（﹣1，0），B（3，0）两点，顶点M关于x轴的对称点是M′．
（1）求抛物线的解析式；
（2）若直线AM′与此抛物线的另一个交点为C，求△CAB的面积；
（3）是否存在过A，B两点的抛物线，其顶点P关于x轴的对称点为Q，使得四边形APBQ为正方形？若存在，求出此抛物线的解析式；若不存在，请说明理由．
（年云南省昆明市）如图，在平面直角坐标系中，抛物线
（
）与x轴交于A、B两点（点A在点B的右侧），与y轴交于点C，点A的坐标为（4，0），抛物线的对称轴是直线
．
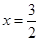（1）求抛物线的解析式；
（2）M为第一象限内的抛物线上的一个点，过点M作MG⊥x轴于点G，交AC于点H，当线段CM=CH时，求点M的坐标；
（3）在（2）的条件下，将线段MG绕点G顺时针旋转一个角α（0°＜α＜90°），在旋转过程中，设线段MG与抛物线交于点N，在线段GA上是否存在点P，使得以P、N、G为顶点的三角形与△ABC相似？如果存在，请求出点P的坐标；如果不存在，请说明理由．
（年青海省西宁市）如图，在平面直角坐标系xOy中，以M为顶点的抛物线与x轴分别相交于B，C两点，抛物线上一点A的横坐标为2，连接AB，AC，正方形DEFG的一边GF在线段BC上，点D，E在线段AB，AC上，AK⊥x轴于点K，交DE于点H，下表给出了这条抛物线上部分点（x，y）的坐标值：
（1）求出这条抛物线的解析式；
（2）求正方形DEFG的边长；
（3）请问在抛物线的对称轴上是否存在点P，在x轴上是否存在点Q，使得四边形ADQP的周长最小？若存在，请求出P，Q两点的坐标；若不存在，请说明理由．
（年蒙自市初中学业水平第一次模拟测试）兴发服装店老板用
元购进一批某款T恤衫，由于深受顾客喜爱，很快售完，老板又用
元购进第二批该款式T恤衫，所购数量与第一批相同，但每件进价比第一批多了
元．
（1）第一批该款式T恤衫每件进价是多少元？
（2）老板以每件
元的价格销售该款式T恤衫，当第二批T恤衫售出
时，出现了滞销，于是决定降价促销，若要使第二批的销售利润不低于
元，剩余的T恤衫每件售价至少要多少元？（利润=售价﹣进价）
（年云南省）为有效开展阳光体育活动，云洱中学利用课外活动时间进行班级篮球比赛，每场比赛都要决出胜负，每队胜一场得2分，负一场得1分．已知九年级一班在8场比赛中得到13分，问九年级一班胜、负场数分别是多少？