（资阳）学校需要购买一批篮球和足球，已知一个篮球比一个足球的进价高30元，买两个篮球和三个足球一共需要510元．
（1）求篮球和足球的单价；
（2）根据实际需要，学校决定购买篮球和足球共100个，其中篮球购买的数量不少于足球数量的
，学校可用于购买这批篮球和足球的资金最多为10500元．请问有几种购买方案？
（3）若购买篮球x个，学校购买这批篮球和足球的总费用为y（元），在（2）的条件下，求哪种方案能使y最小，并求出y的最小值．
在△ABC中，AC=BC=2，∠C=90°．将一块三角板的直角顶点放在斜边AB的中点P处，将三角板绕点P旋转，三角板的两直角边分别交边AC、CB于点D、E．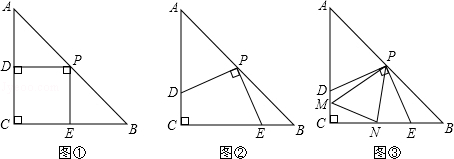
（1）如图①，当PD⊥AC时，则DC+CE的值是 ．
（2）如图②，当PD与AC不垂直时，（1）中的结论是否还成立？若成立，请予以证明；若不成立，请说明理由；
（3）如图③，在∠DPE内作∠MPN=45°，使得PM、PN分别交DC、CE于点M、N，连接MN．那么△CMN的周长是否为定值？若是，求出定值；若不是，请说明理由．
如图，A、P、B、C是⊙O上的四点，∠APC=∠CPB=60°，过点C作CM∥BP交PA的延长线于点M．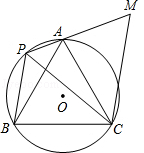
（1）求证：△ACM≌△BCP；
（2）若PA=1，PB=2，求△PCM的面积．
已知：⊙O的半径长为5，点A、B、C在⊙O上，AB=BC=6，点E在射线BC上．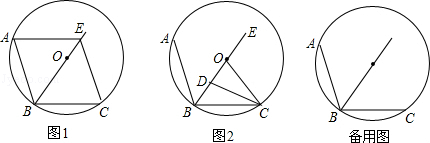
（1）如图1，联结AE、CE，求证：AE=CE；
（2）如图2，以点C为圆心，CO为半径画弧交半径OB于D，求BD的长．
（3）当OE=
时，求线段AE的长．
在平面直角坐标系xOy（如图）中，已知A（﹣1，3），B（2，n）两点在二次函数y=﹣
x2+bx+4的图象上．
（1）求b与n的值；
（2）联结OA、OB、AB，求△AOB的面积；
（3）若点P（不与点A重合）在题目中给出的二次函数的图象上，且∠POB=45°，求点P的坐标．
四边形ABCD是平行四边形，E是对角线AC上一点，射线DE分别交射线CB、AB于点F、G．
（1）如图，如果点F在CB边上，点G在AB边的延长线上，求证：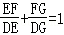
；
（2）如果点F在CB边的延长线上，点G在AB边上，试写出
与
之间的一种等量关系，并给出证明．