(资阳)学校需要购买一批篮球和足球,已知一个篮球比一个足球的进价高30元,买两个篮球和三个足球一共需要510元.
(1)求篮球和足球的单价;
(2)根据实际需要,学校决定购买篮球和足球共100个,其中篮球购买的数量不少于足球数量的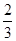 ,学校可用于购买这批篮球和足球的资金最多为10500元.请问有几种购买方案?
,学校可用于购买这批篮球和足球的资金最多为10500元.请问有几种购买方案?
(3)若购买篮球x个,学校购买这批篮球和足球的总费用为y(元),在(2)的条件下,求哪种方案能使y最小,并求出y的最小值.
猕猴嬉戏是王屋山景区的一大特色,猕猴玩偶非常畅销.小李在某网店选中 , 两款猕猴玩偶,决定从该网店进货并销售.两款玩偶的进货价和销售价如下表:
|
类别 价格 |
款玩偶 |
款玩偶 |
|
进货价(元 个) |
40 |
30 |
|
销售价(元 个) |
56 |
45 |
(1)第一次小李用1100元购进了 , 两款玩偶共30个,求两款玩偶各购进多少个.
(2)第二次小李进货时,网店规定 款玩偶进货数量不得超过 款玩偶进货数量的一半.小李计划购进两款玩偶共30个,应如何设计进货方案才能获得最大利润,最大利润是多少?
(3)小李第二次进货时采取了(2)中设计的方案,并且两次购进的玩偶全部售出,请从利润率的角度分析,对于小李来说哪一次更合算?
(注:利润率
在古代,智慧的劳动人民已经会使用“石磨”,其原理为在磨盘的边缘连接一个固定长度的“连杆”,推动“连杆”带动磨盘转动,将粮食磨碎,物理学上称这种动力传输工具为“曲柄连杆机构”.
小明受此启发设计了一个“双连杆机构”,设计图如图1,两个固定长度的“连杆” , 的连接点 在 上,当点 在 上转动时,带动点 , 分别在射线 , 上滑动, .当 与 相切时,点 恰好落在 上,如图2.
请仅就图2的情形解答下列问题.
(1)求证: ;
(2)若 的半径为5, ,求 的长.

开凿于北魏孝文帝年间的龙门石窟是中国石刻艺术瑰宝,卢舍那佛像是石窟中最大的佛像.某数学活动小组到龙门石窟景区测量这尊佛像的高度.如图,他们选取的测量点 与佛像 的底部 在同一水平线上.已知佛像头部 为 ,在 处测得佛像头顶部 的仰角为 ,头底部 的仰角为 ,求佛像 的高度(结果精确到 .参考数据: , , .

如图,大、小两个正方形的中心均与平面直角坐标系的原点 重合,边分别与坐标轴平行,反比例函数 的图象与大正方形的一边交于点 ,且经过小正方形的顶点 .
(1)求反比例函数的解析式;
(2)求图中阴影部分的面积.

2021年4月,教育部印发《关于进一步加强中小学生睡眠管理工作的通知》,明确要求初中生每天睡眠时间应达到9小时.某初级中学为了解学生睡眠时间的情况,从本校学生中随机抽取500名进行问卷调查,并将调查结果用统计图描述如下.
|
调查问卷 1.近两周你平均每天睡眠时间大约是______小时. 如果你平均每天睡眠时间不足9小时,请回答第2个问题 2.影响你睡眠时间的主要原因是______(单选). .校内课业负担重 .校外学习任务重 .学习效率低 .其他 |
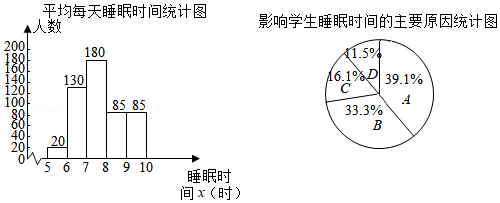
平均每天睡眠时间 (时 分为5组:① ;② ;③ ;④ ;⑤ .
根据以上信息,解答下列问题:
(1)本次调查中,平均每天睡眠时间的中位数落在第 (填序号)组,达到9小时的学生人数占被调查人数的百分比为 ;
(2)请对该校学生睡眠时间的情况作出评价,并提出两条合理化建议.