(成都)(本小题满分10分)已知AC,EC分别为四边形ABCD和EFCG的对角线,点E在△ABC内,∠CAE+∠CBE=90.
(1)如图①,当四边形ABCD和EFCG均为正方形时,连接BF.
i)求证:△CAE∽△CBF;
ii)若BE=1,AE=2,求CE的长;
(2)如图②,当四边形ABCD和EFCG均为矩形,且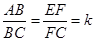 时,若BE=1,AE=2,CE=3,求k的值;
时,若BE=1,AE=2,CE=3,求k的值;
(3)如图③,当四边形ABCD和EFCG均为菱形,且∠DAB=∠GEF=45°时,设BE=m,AE=n,CE=p,试探究m,n,p三者之间满足的等量关系.(直接写出结果,不必写出解答过程)
今年我国许多地方严重的“旱情”,为了鼓励居民节约用水,区政府计划实行两级收费制,即每月用水量不超过14吨(含14吨)时,每吨按政府补贴优惠价收费;每月超过14吨时,超过部分每吨按市场调节价收费.小英家1月份用水20吨,交水费29元;2月份用水18吨,交水费24元.
(1)求每吨水的政府补贴优惠价和市场调节价分别是多少?
(2)设每月用水量为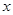 吨,应交水费为y元,写出y与
吨,应交水费为y元,写出y与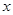 之间的函数关系式;
之间的函数关系式;
(3)小英家3月份交水费39元,她家应用水多少吨?
如图,有一块圆形铁皮,BC是⊙O的直径,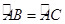 ,在此圆形铁皮中剪下一个扇形(阴影部分).
,在此圆形铁皮中剪下一个扇形(阴影部分).
(1)当⊙O的半径为2时,求这个扇形(阴影部分)的面积(结果保留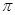 );
);
(2)当⊙O的半径为R(R>0)时,在剩下的三块余料中,能否从第③块余料中剪出一个圆作为底面与此扇形
围成一个圆锥?请说明理由.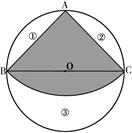
“江宁义乌小商品城”销售某种小商品,平均每天可销售30件,每件盈利50元. 为了尽快减少库存,销售商决定采取降价措施. 经调查发现,每件商品每降价1元,平均每天可多售出2件.设每件商品降价x元. 据此规律,请回答:
(1)日销售量增加件,每件商品盈利元(用含x的代数式表示);
(2)在上述条件不变、销售正常情况下,每件商品降价多少元时,销售商日盈利可达到2100元?
下图是一座人行天桥的示意图,天桥的高CB为10米,坡面CA的坡角为30°.为了方便行人推车过桥,市政部门决定降低坡度,使新坡面CD的坡角为18°,若新桥脚前需留4米的人行道,问离原坡脚15米的花坛是否需要拆除?请说明理由.
(参考数据:sinl8°≈0.3090,cosl8°≈0.9511,tanl8°≈0.3249,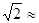 1.414,
1.414,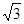 ≈1.732)
≈1.732)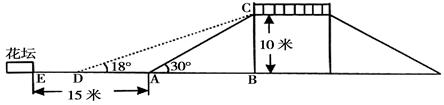
在一个不透明的口袋中装有4张相同的纸牌,它们分别标有数字1、2、3、4.小明先从口袋里随机取出一张纸牌,记下数字为x;再由小华从剩下的3张纸牌中随机取出一张纸牌,记下数字为y.
(1)用列表法或画树状图表示出(x,y)的所有可能出现的结果;
(2)求小明、小华各取一张纸牌所确定的点(x,y)落在反比例函数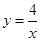 的图象上的概率.
的图象上的概率.