(资阳)学校需要购买一批篮球和足球,已知一个篮球比一个足球的进价高30元,买两个篮球和三个足球一共需要510元.
(1)求篮球和足球的单价;
(2)根据实际需要,学校决定购买篮球和足球共100个,其中篮球购买的数量不少于足球数量的 ,学校可用于购买这批篮球和足球的资金最多为10500元.请问有几种购买方案?
,学校可用于购买这批篮球和足球的资金最多为10500元.请问有几种购买方案?
(3)若购买篮球x个,学校购买这批篮球和足球的总费用为y(元),在(2)的条件下,求哪种方案能使y最小,并求出y的最小值.
 、
、 两组卡片共5张,
两组卡片共5张, 中三张分别写有数字2,4,6,
中三张分别写有数字2,4,6,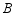 中两张分别写有3,5,它们除数字外没有任何区别.
中两张分别写有3,5,它们除数字外没有任何区别.
(1)随机地从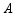 中抽取一张,求抽到数字为2的概率;
中抽取一张,求抽到数字为2的概率;
(2)随机地分别从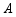 、
、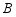 中各抽取一张,请你用画树状图或列表的方法表示所有等可能的结果.现制定这样一个游戏规则:若所选出的两数之积为3的倍数,则甲获胜;否则乙获胜.请问这样的游戏规则对甲乙双方公平吗?为什么?
中各抽取一张,请你用画树状图或列表的方法表示所有等可能的结果.现制定这样一个游戏规则:若所选出的两数之积为3的倍数,则甲获胜;否则乙获胜.请问这样的游戏规则对甲乙双方公平吗?为什么?
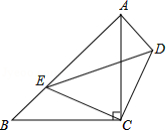
如图,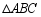 、
、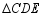 均为等腰直角三角形,
均为等腰直角三角形,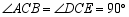 ,点
,点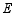 在
在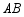 上.求证:
上.求证: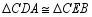 .
.
如图,抛物线
的顶点为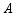 ,与
,与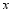 轴的正半轴交于点
轴的正半轴交于点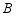 .
.
(1)将抛物线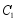 上的点的横坐标和纵坐标都扩大到原来的2倍,求变换后得到的抛物线的解析式;
上的点的横坐标和纵坐标都扩大到原来的2倍,求变换后得到的抛物线的解析式;
(2)将抛物线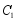 上的点
上的点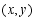 变为
变为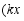 ,
,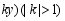 ,变换后得到的抛物线记作
,变换后得到的抛物线记作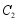 ,抛物线
,抛物线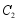 的顶点为
的顶点为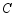 ,点
,点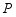 在抛物线
在抛物线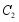 上,满足
上,满足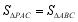 ,且
,且 .
.
①当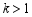 时,求
时,求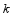 的值;
的值;
②当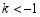 时,请直接写出
时,请直接写出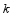 的值,不必说明理由.
的值,不必说明理由.
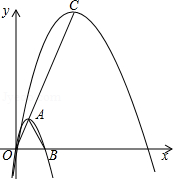
若正方形有两个相邻顶点在三角形的同一条边上,其余两个顶点分别在三角形的另两条边上,则正方形称为三角形该边上的内接正方形, 中,设
中,设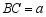 ,
, ,
,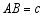 ,各边上的高分别记为
,各边上的高分别记为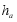 ,
,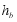 ,
, ,各边上的内接正方形的边长分别记为
,各边上的内接正方形的边长分别记为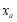 ,
, ,
,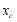
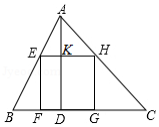
(1)模拟探究:如图,正方形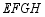 为
为 的
的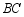 边上的内接正方形,求证:
;
边上的内接正方形,求证:
;
(2)特殊应用:若 ,
,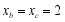 ,求
的值;
,求
的值;
(3)拓展延伸:若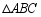 为锐角三角形,
为锐角三角形, ,请判断
,请判断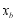 与
与 的大小,并说明理由.
的大小,并说明理由.
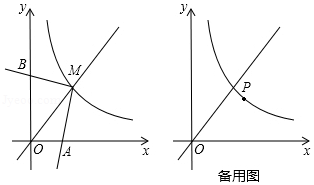
如图,反比例函数
的图象与直线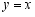 交于点
交于点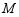 ,
,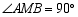 ,其两边分别与两坐标轴的正半轴交于点
,其两边分别与两坐标轴的正半轴交于点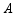 ,
,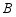 ,四边形
,四边形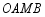 的面积为6.
的面积为6.
(1)求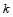 的值;
的值;
(2)点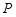 在反比例函数
的图象上,若点
在反比例函数
的图象上,若点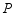 的横坐标为3,
的横坐标为3,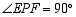 ,其两边分别与
,其两边分别与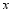 轴的正半轴,直线
轴的正半轴,直线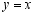 交于点
交于点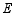 ,
,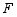 ,问是否存在点
,问是否存在点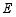 ,使得
,使得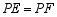 ?若存在,求出点
?若存在,求出点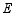 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.