阅读理解
抛物线y= x2上任意一点到点(0,1)的距离与到直线y=﹣1的距离相等,你可以利用这一性质解决问题.
x2上任意一点到点(0,1)的距离与到直线y=﹣1的距离相等,你可以利用这一性质解决问题.
问题解决
如图,在平面直角坐标系中,直线y=kx+1与y轴交于C点,与函数y= x2的图象交于A,B两点,分别过A,B两点作直线y=﹣1的垂线,交于E,F两点.
x2的图象交于A,B两点,分别过A,B两点作直线y=﹣1的垂线,交于E,F两点.
(1)写出点C的坐标,并说明∠ECF=90°;
(2)在△PEF中,M为EF中点,P为动点.
①求证:PE2+PF2=2(PM2+EM2);
②已知PE=PF=3,以EF为一条对角线作平行四边形CEDF,若1<PD<2,试求CP的取值范围.
某商店采购了某品牌的T恤、衬衫、裤子共60件,每款服装按进价至少要购进10件,且恰好用完所带的进货款3700元.设购进T恤x件,衬衫y件.三款服装的进价和预售价如下表: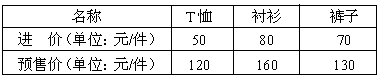
(1)求出y与x之间的函数关系式;
(2)假设所购进服装全部售出,该商店在采购和销售的过程中需支出各种费用共300元.
①求出预估利润W(元)与T恤x(件)的函数关系式;(注:预估利润W=预售总额-进货款-各种费用)
②求出预估利润的最大值,并写出此时对应购进各款服装多少件.
如图,已知∠A,请你仅用尺规,按下列要求作图和计算(不必写画法):
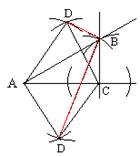
(1)选取适当的边长,在所给的∠A图形上画一个含∠A 的直角三角形ABC,并标上字母,其中点C为直角顶点,点B为另一锐角顶点;
(2)以AC为一边作等边△ACD;
(3)若设∠A=30°、BC边长为a,则BD的长为.
PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物,对人体健康和大气环境质量的影响更大. 2012年2月,国务院同意发布新修订的《环境空气质量标准》增加了PM2.5监测指标. 我国PM2.5标准采用世卫组织(WHO)设定最宽限值:即日平均浓度小于75微克/立方米为安全值,而WHO标准为日平均浓度值小于25微克/立方米是安全值. 根据某市40个国控监测点某日PM2.5监测数据,绘制成如下所示的频数分布表.
根据表中提供的信息解答下列问题:
(1) 频数分布表中的a=, b=, c=;
(2) 补充完整答题卡上的频数分布直方图;
(3)在40个国控监测点中,这天的PM2.5日平均浓度值符合我国PM2.5标准安全值的监测点所占比例是;
(4) 如果全市共有100个测量点,那么这天的PM2.5日平均浓度值符合WHO标准安全值的监测点约有多少个?
如图,反比例函数 (k≠0)经过点A,连结OA,设OA与x轴的夹角为
(k≠0)经过点A,连结OA,设OA与x轴的夹角为 .
.
(1)求反比例函数解析式;
(2)若点B是反比例函数图象上的另一点,且点B的横坐标为sin ,请你求出sin
,请你求出sin 的值后,写出点B的坐标,并在图中画出点B的大致位置.
的值后,写出点B的坐标,并在图中画出点B的大致位置.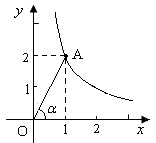
已知抛物线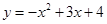 交y轴于点A,交x轴于点B,C(点B在点C的右侧).过点A作垂直于y轴的直线l. 在位于直线l下方的抛物线上任取一点P,过点P作直线PQ平行于y轴交直线l于点Q.连接AP.
交y轴于点A,交x轴于点B,C(点B在点C的右侧).过点A作垂直于y轴的直线l. 在位于直线l下方的抛物线上任取一点P,过点P作直线PQ平行于y轴交直线l于点Q.连接AP.
(1)写出A,B,C三点的坐标;
(2)若点P位于抛物线的对称轴的右侧:
①如果以A,P,Q三点构成的三角形与△AOC相似,求出点P的坐标;
②若将△APQ沿AP对折,点Q的对应点为点M.是否存在点P,使得点M落在x轴上.若存在,求出点P的坐标;若不存在,请说明理由.