(年青海省中考)为了解全校学生上学的交通方式,该校九年级(8)班的5名同学联合设计了一份调查问卷,对该校部分学生进行了随机调查.按A(骑自行车)、B(乘公交车)、C(步行)、D(乘私家车)、E(其他方式)设置选项,要求被调查同学从中单选.并将调查结果绘制成条形统计图1和扇形统计图2,根据以上信息,解答下列问题:

(1)本次接受调查的总人数是 人,并把条形统计图补充完整;
(2)在扇形统计图中,“步行”的人数所占的百分比是 ,“其他方式”所在扇形的圆心角度数是 ;
(3)已知这5名同学中有2名女同学,要从中选两名同学汇报调查结果.请你用列表法或画树状图的方法,求出恰好选出1名男生和1名女生的概率.
如图在△ABC和△DCE中,AC=BC,DC=EC,∠ACB=∠DCE=90°,将△DCE绕点C旋转(0°<∠ACD<180°),连结BD和AE:
(1)求证:△BCD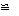 △ACE;
△ACE;
(2)试确定线段BD和AE的数量关系和位置关系;
如图所示,已知BD为△ABC的角平分线,CD为△ABC外角∠ACE的平分线,且与BD交于点D;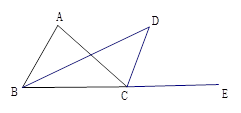
(1)若∠ABC=60°,∠DCE=70°,则∠D= °;
(2)若∠ABC=70°,∠A=80°,则∠D= °;
(3)当∠ABC和∠ACB在变化,而∠A始终保持不变,则∠D是否发生变化?为什么?由此你能得出什么结论?(用含∠A的式子表示∠D)
如图所示,已知AD是∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,且BD=CD.求证:BE=CF.
如图,△ABC中,AB=AC=CD,BD=AD,求△ABC中各角的度数。
如图,AD和CB相交于点O,且AB∥CD,OA=OB.求证:OC=OD.