如图,四边形ABCD为平行四边形,四边形ADEF是正方形,且BD⊥平面CDE,H是BE的中点,G是AE,DF的交点.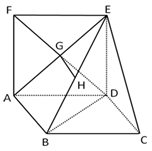
(1)求证:GH∥平面CDE;
(2)求证:面ADEF⊥面ABCD.
已知函数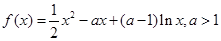 ,
,
(1)讨论函数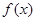 的单调性;
的单调性;
(2)证明:若 ,则对于任意
,则对于任意 有
有 。
。
某厂家拟在2013年举行促销活动,经调查测算,该产品的年销售量(即该厂的年产量) 万件与年促销费用
万件与年促销费用 万元满足
万元满足 (
( 为常数),如果不搞促销活动,则该产品的年销售量是1万件. 已知2013年生产该产品的固定投入为8万元,每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的
为常数),如果不搞促销活动,则该产品的年销售量是1万件. 已知2013年生产该产品的固定投入为8万元,每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的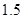 倍(产品成本包括固定投入和再投入两部分资金,不包括促销费用).
倍(产品成本包括固定投入和再投入两部分资金,不包括促销费用).
(1)将2013年该产品的利润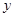 万元表示为年促销费用
万元表示为年促销费用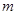 万元的函数;
万元的函数;
(2)该厂家2013年的促销费用投入多少万元时,厂家的利润最大?
已知函数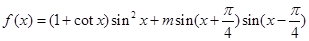 ,
,
(1)当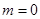 时,求
时,求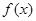 在区间
在区间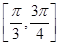 上的取值范围;
上的取值范围;
(2)当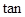
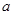 =2时,
=2时,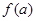 =
= ,求
,求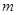 的值。
的值。
已知命题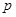 :方程
:方程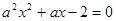 在[-1,1]上有解;命题
在[-1,1]上有解;命题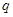 :只有一个实数
:只有一个实数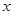 满足不等式
满足不等式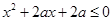 ,若命题“p或q”是假命题,求实数a的取值范围.
,若命题“p或q”是假命题,求实数a的取值范围.
已知函数 ,设曲线
,设曲线 在与
在与 轴交点处的切线为
轴交点处的切线为 ,
, 为
为 的导函数,满足
的导函数,满足 .
.
(1)求 ;
;
(2)设 ,
, ,求函数
,求函数 在
在 上的最大值;
上的最大值;
(3)设 ,若对于一切
,若对于一切 ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.