在平面直角坐标系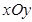 中,已知曲线
中,已知曲线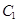 上的任意一点到点A(-1,0),B(1,0)的距离之和为
上的任意一点到点A(-1,0),B(1,0)的距离之和为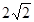
(Ⅰ)求曲线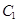 的方程;
的方程;
(Ⅱ)设椭圆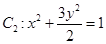 ,若斜率为
,若斜率为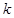 的直线
的直线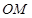 交椭圆
交椭圆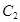 于点
于点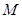 ,垂直于
,垂直于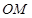 的直线
的直线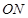 交曲线
交曲线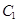 于点
于点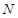 ,求证:
,求证: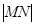 的最小值为
的最小值为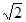 .
.
在平面直角坐标系xOy中,直线l的参数方程为 (t为参数),它与曲线C:(y-2)2-x2=1交于A、B两点.
(t为参数),它与曲线C:(y-2)2-x2=1交于A、B两点.
(1)求|AB|的长;
(2)以O为极点,x轴的正半轴为极轴建立极坐标系,设点P的极坐标为 ,求点P到线段AB中点M的距离.
,求点P到线段AB中点M的距离.
在直角坐标系xOy中,以O为极点,x轴正半轴为极轴建立极坐标系.圆C1,直线C2的极坐标方程分别为ρ=4sin θ,ρcos  =2
=2 .
.
(1)求C1与C2交点的极坐标;
(2)设P为C1的圆心,Q为C1与C2交点连线的中点.已知直线PQ的参数方程为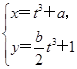 (t∈R为参数),求a,b的值.
(t∈R为参数),求a,b的值.
已知曲线C的极坐标方程为ρ=4cos θ,以极点为原点,极轴为x轴正半轴建立平面直角坐标系,设直线l的参数方程为 (t为参数).
(t为参数).
(1)求曲线C的直角坐标方程与直线l的普通方程;
(2)设曲线C与直线l相交于P,Q两点,以PQ为一条边作曲线C的内接矩形,求该矩形的面积.
设直线l过点P(-3,3),且倾斜角为 .
.
(1)写出直线l的参数方程;
(2)设此直线与曲线C: (θ为参数)交于A,B两点,求|PA|·|PB|.
(θ为参数)交于A,B两点,求|PA|·|PB|.
在平面直角坐标系xOy中,直线l的参数方程为 (t为参数),曲线C的参数方程为
(t为参数),曲线C的参数方程为 (θ为参数).试求直线l和曲线C的普通方程,并求出它们的公共点的坐
(θ为参数).试求直线l和曲线C的普通方程,并求出它们的公共点的坐