四棱锥A-BCDE的正视图和俯视图如下,其中正视图是等边三角形,俯视图是直角梯形.
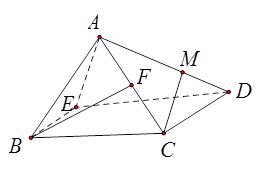
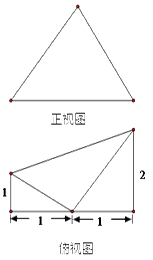
(Ⅰ)若F为AC的中点,当点M在棱AD上移动,是否总有BF丄CM,请说明理由.
(Ⅱ)求三棱锥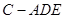 的高.
的高.
在直角坐标系 中,点p到两点
中,点p到两点 的距离之和等于4,
的距离之和等于4,
设点P的轨迹为C,直线 与C交于A、B两点,
与C交于A、B两点,
(1)写出C的方程;
(2)若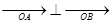 ,求k的值。
,求k的值。
设函数 .
.
(1)求不等式 的解集;
的解集;
(2)若不等式 的解集是非空的集合,求实数
的解集是非空的集合,求实数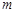 的取值范围.
的取值范围.
以平面直角坐标系的坐标原点为极点, 轴的非负半轴为极轴建立极坐标系,曲线E的极坐标方程为
轴的非负半轴为极轴建立极坐标系,曲线E的极坐标方程为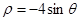 ,曲线F的参数方程为
,曲线F的参数方程为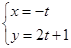 (t为参数)
(t为参数)
(1) 求曲线E的直角坐标方程及曲线F的普通方程;
(2)判断两直线的位置关系,若相交,求弦长,若不相交,说明理由。
如图,已知⊙O和⊙M相交于A.B两点,AD为⊙M的直径,直线BD交⊙O于点C,点G为弧BD中点,连结AG分别交⊙O.BD于点E.F连结CE。
(Ⅰ)求证: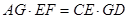 ;
;
(Ⅱ)求证: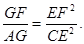

在直角坐标系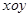 中,点p到两点
中,点p到两点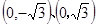 的距离之和等于4,设点P的轨迹为C,直线
的距离之和等于4,设点P的轨迹为C,直线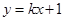 与C交于A、B两点,
与C交于A、B两点,
(1)写出C的方程;
(2)若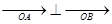 ,求k的值。
,求k的值。