如图,在正方形网格中,△ABC各顶点都在格点上,点A,C的坐标分别为(﹣5,1)、(﹣1,4),结合所给的平面直角坐标系解答下列问题:

(1)画出△ABC关于y轴对称的△A1B1C1;
(2)画出△ABC关于原点O对称的△A2B2C2;
(3)点C1的坐标是 ;点C2的坐标是 ;
(4)试判断: 与
与 是否关于x轴对称?(只需写出判断结果) .
是否关于x轴对称?(只需写出判断结果) .
如图,已知二次函数 的图象经过点 ,与 轴交于点 .在 轴上有一动点 , ,过点 作 轴的垂线交直线 于点 ,交该二次函数图象于点 .
(1)求 的值和直线 的解析式;
(2)过点 作 于点 ,设 , 的面积分别为 , ,若 ,求 的值;
(3)点 是该二次函数图象上位于第一象限的动点,点 是线段 上的动点,当四边形 是平行四边形,且 周长取最大值时,求点 的坐标.

如图,已知 , 是 的直径,过点 作 的切线交 的延长线于点 , 的弦 交 于点 ,且 .
(1)求证: ;
(2)连接 交 于点 ,过点 作 于点 ,若 , ,求 的长.

一次函数 的图象经过点 , .
(1)求该一次函数的解析式;
(2)如图,该一次函数的图象与反比例函数 的图象相交于点 , , , ,与 轴交于点 ,且 ,求 的值.
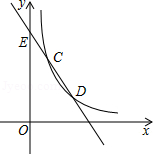
如图,甲建筑物 ,乙建筑物 的水平距离 为 ,且乙建筑物的高度是甲建筑物高度的6倍,从 , , 在同一水平线上)点测得 点的仰角为 ,测得 点的仰角为 ,求这两座建筑物顶端 、 间的距离(计算结果用根号表示,不取近似值).
某图书馆计划选购甲、乙两种图书.已知甲图书每本价格是乙图书每本价格的2.5倍,用800元单独购买甲图书比用800元单独购买乙图书要少24本.
(1)甲、乙两种图书每本价格分别为多少元?
(2)如果该图书馆计划购买乙图书的本数比购买甲图书本数的2倍多8本,且用于购买甲、乙两种图书的总经费不超过1060元,那么该图书馆最多可以购买多少本乙图书?