计算下列各题
(1)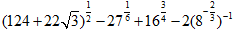 ;
;
(2)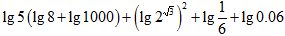
已知函数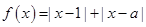 .
.
(1)若a=2,解不等式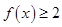 ;
;
(2)若a>1,任意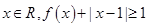 ,求实数a的取值范围.
,求实数a的取值范围.
平面直角坐标系中,直线l的参数方程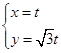 (t为参数),以坐标原点为极点,x轴的正半轴为极轴,建立极坐标系,已知曲线C的极坐标方程为
(t为参数),以坐标原点为极点,x轴的正半轴为极轴,建立极坐标系,已知曲线C的极坐标方程为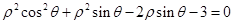
(1)求直线l的极坐标方程;
(2)若直线l与曲线C相交于A,B两点,求|AB|.
如图,AB是圆O的直径,弦CD⊥AB于点M,E是CD延长线上一点,AB=10,CD=8,3ED=4OM,EF切圆O于F,BF交CD于G.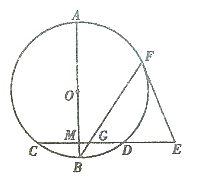
(1)求证:△EFG为等腰三角形;
(2)求线段MG的长.
如图,椭圆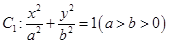 和圆
和圆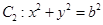 ,已知椭圆
,已知椭圆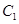 过点
过点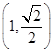 ,焦距为2.
,焦距为2.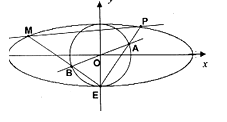
(1)求椭圆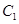 的方程;
的方程;
(2)椭圆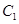 的下顶点为E,过坐标原点O且与坐标轴不重合的任意直线l与圆
的下顶点为E,过坐标原点O且与坐标轴不重合的任意直线l与圆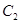 相交于点A,B,直线EA,EB与椭圆
相交于点A,B,直线EA,EB与椭圆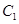 的另一个交点分别是点P,M,设PM的斜率为
的另一个交点分别是点P,M,设PM的斜率为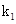 ,直线l的斜率为
,直线l的斜率为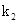 ,求
,求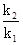 的值
的值