已知函数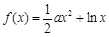 ,
,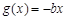 ,设
,设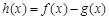 .
.
(1)若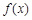 在
在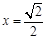 处取得极值,且
处取得极值,且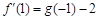 ,求函数
,求函数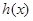 的单调区间;
的单调区间;
(2)若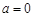 时,函数
时,函数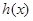 有两个不同的零点
有两个不同的零点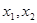 .求证:
.求证: .
.
已知函数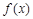 满足2
满足2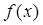 +
+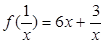 ,对x≠0恒成立,在数列{an}、{bn}中,a1=1,b1=1,对任意x∈N+,
,对x≠0恒成立,在数列{an}、{bn}中,a1=1,b1=1,对任意x∈N+,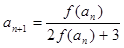 ,
,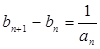 。
。
(1)求函数 解析式;
解析式;
(2)求数列{an}、{bn}的通项公式;
(3)若对任意实数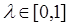 ,总存在自然数k,当n≥k时,
,总存在自然数k,当n≥k时,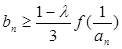 恒成立,求k的最小值。
恒成立,求k的最小值。
已知点P(2,1)在抛物线C1:x2=2py(p>0)上,直线l过点Q(0,2)且与抛物线C1交于A、B两点.
(1)求抛物线C1的方程及弦AB中点M的轨迹C2的方程;
(2)若直线l1、l2分别为C1、C2的切线,且l1∥l2,求l1到l2的最近距离.
某工厂某种产品的年产量为1000x件,其中x∈[20,100],需要投入的成本为C(x),当x∈[20,80]时,C(x)=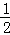 x2﹣30x+500(万元);当x∈(80,100]时,C(x)=
x2﹣30x+500(万元);当x∈(80,100]时,C(x)=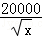 (万元).若每一件商品售价为
(万元).若每一件商品售价为 (万元),通过市场分析,该厂生产的商品能全部售完.
(万元),通过市场分析,该厂生产的商品能全部售完.
(1)写出年利润L(x)(万元)关于x的函数解析式;
(2)年产量为多少件时,该厂在这一商品的生产中所获利润最大?
如图,四棱锥P﹣ABCD的底面是菱形,∠ABC=60°,PA⊥底面ABCD,E,F分别是BC,PC的中点,点H在PD上,且EH⊥PD,PA=AB=2.
(1)求证:EH∥平面PBA;
(2)求三棱锥P﹣AFH的体积.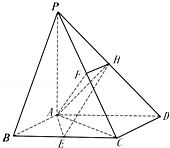
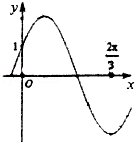
已知如图为函数f(x)=2sin(ωx+φ)(ω>0,0<φ<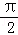 )的部分图象.
)的部分图象.
(1)求f(x)的解析式及其单调递增区间;
(2)求函数g(x)= 的值域.
的值域.