已知数列 的前
的前 项和为
项和为 ,且满足
,且满足 .
.
(1)求 ,
, 的值;
的值;
(2)求 ;
;
(3)设 ,数列
,数列 的前
的前 项和为
项和为 ,求证:
,求证: .
.
如图,已知四棱锥S—ABCD中,△SAD是边长为a的正三角形,平面SAD⊥平面ABCD,四边形ABCD为菱形,∠DAB=60°,P为AD中点,Q为SB中点,(1)求证:PQ∥平面SCD;(2)求二面角B—PC—Q的正切值的大小。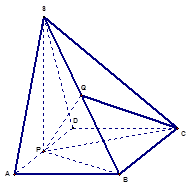
如图所示,在长方体OABC—O1A1B1C1中,OA=2,AB=3,AA1=2。作OD⊥AC于D,利用空间坐标系求点O1到点D的距离。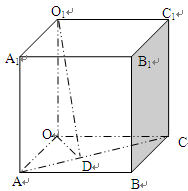
长方体的全面积为11,十二条棱长度之和为24,求这个长方体的一条对角线长。
已知两圆C1:x2+y2="4," C2: x2+y2-2x-4y+4=0,直线l: x+2y="0," 求经过圆C1和C2的交点且和直线l相切的圆的方程。
已知命题P:方程x2+mx+1=0有两个不等的负实根;命题Q:方程4x2+4(m-2)x+1=0无实根,若“P或Q”为真,而“P且Q”为假。求实数m的取值范围。