【选修4-2:极坐标与参数方程】已知直线n的极坐标是 ,圆A的参数方程是
,圆A的参数方程是 (θ是参数)
(θ是参数)
(1)将直线n的极坐标方程化为普通方程;
(2)求圆A上的点到直线n上点距离的最小值.
在长方体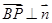 中,
中, ,
, ,
,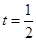 为
为 中点.(Ⅰ)证明:
中点.(Ⅰ)证明: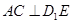 ;(Ⅱ)求
;(Ⅱ)求 与平面
与平面 所成角的正弦值;(Ⅲ)在棱
所成角的正弦值;(Ⅲ)在棱 上是否存在一点
上是否存在一点 ,使得
,使得 ∥平面
∥平面 ?若存在,求
?若存在,求 的长;若不存在,说明理由.
的长;若不存在,说明理由.
抽签方式决定出场顺序.通过预赛,选拔出甲、乙等五支队伍参加决赛.
(Ⅰ)求决赛中甲、乙两支队伍恰好排在前两位的概率;
(Ⅱ)若决赛中甲队和乙队之间间隔的队伍数记为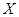 ,求
,求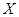 的分布列和数学期望.
的分布列和数学期望.
已知函数
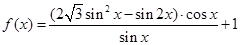 .
.
(Ⅰ)求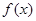 的定义域及最小正周期;
的定义域及最小正周期;
(Ⅱ)求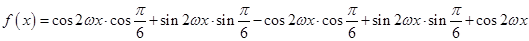
在区间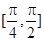 上的最值.
上的最值.
如图所示,O为坐标原点,过点P(2,0)且斜率为k的直线L交抛物线y =2x于M(x
=2x于M(x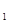 ,y
,y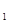 ),N(x
),N(x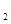 ,y
,y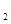 )两点. ⑴写出直线L的方程;⑵求x
)两点. ⑴写出直线L的方程;⑵求x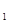 x
x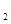 与y
与y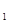 y
y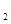 的值;⑶求证:OM⊥ON
的值;⑶求证:OM⊥ON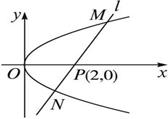
已知函数f(x)=-x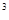 +3x
+3x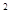 +9x+a
+9x+a
⑴求f(x)的单调递减区间;⑵若f(x)在区间[-2,2]上的最大值为20,求它在该区间上的最小值。