已知椭圆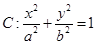
 的离心率为
的离心率为 ,以原点为圆心,椭圆的短半轴为半径的圆与直线
,以原点为圆心,椭圆的短半轴为半径的圆与直线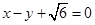 相切,过点
相切,过点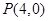 且不垂直于x轴直线
且不垂直于x轴直线 与椭圆C相交于A、B两点.
与椭圆C相交于A、B两点.
(1)求椭圆C的方程;
(2)求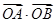 的取值范围;
的取值范围;
(3)若B点关于x轴的对称点是E,证明:直线AE与x轴相交于定点.
(本小题满分13分)已知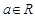 ,函数
,函数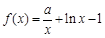 ,
,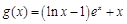 .
.
(1)判断函数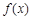 在
在 区间
区间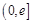 上的单调性(其中
上的单调性(其中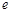 为自然对数的
为自然对数的 底数);
底数);
(2)是否存在实数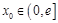 ,使曲线
,使曲线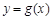 在点
在点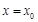 处的切线与
处的切线与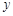 轴垂直
轴垂直
若存在,求出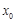 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
本小题满分12分)如图菱形 的边长为
的边长为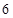 ,
,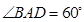 ,
,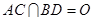 .将菱形
.将菱形 沿对角线
沿对角线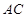 折起,得到三棱锥
折起,得到三棱锥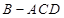 ,
, 点
点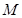 是棱
是棱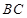 的中点,
的中点,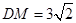 .
.
(1) 求证: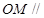 平面
平面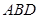 ;
;
(2) 求证:平面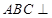 平面
平面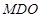 ;
;
(3) 求三棱锥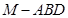 的体积.
的体积.
(本小题满分12分)已知直线 :
: 与直线
与直线 :
: 互相平行,经过点
互相平行,经过点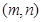 的直线
的直线 与
与 ,
, 垂直,且被
垂直,且被 ,
, 截得的线段长为
截得的线段长为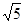 ,试求直线
,试求直线 的方程.
的方程.
(本小题满分12分) 已知函数
已知函数 .
.
(1)设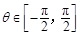 ,且
,且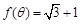 ,求
,求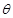
 的值;
的值;
(2)在△ABC中,AB=1, ,且△ABC面积为
,且△ABC面积为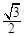 ,求sinA+sinB的值.
,求sinA+sinB的值.
题号:04
“矩阵与变换和坐标系与参数方程”模块(10分)
在极坐标系中,极点为A,已知“葫芦”型封闭曲线 由圆弧ACB和圆弧BDA组成.已知
由圆弧ACB和圆弧BDA组成.已知
(1)求圆弧ACB和圆弧BDA的极坐标方程;
(2)求曲线 围成的区域面积.
围成的区域面积.