已知函数 .
.
(Ⅰ)当 时,求函数
时,求函数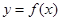 的单调区间;
的单调区间;
(Ⅱ) 时,令
时,令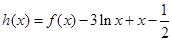 .求
.求 在
在 上的最大值和最小值;
上的最大值和最小值;
(Ⅲ)若函数 对
对 恒成立,求实数
恒成立,求实数 的取值范围
的取值范围
(本小题为选做题,满分10分)
设点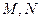 分别是曲线
分别是曲线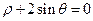 和
和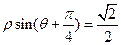 上的动点,求动点
上的动点,求动点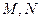 间的最小距离.
间的最小距离.
(本小题为选做题,满分10分)
已知矩阵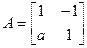 ,其中
,其中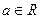 ,若点P(1,1)在矩阵A的变换下得到点
,若点P(1,1)在矩阵A的变换下得到点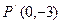 ,
,
(1)求实数a的值;(2)求矩阵A的特征值及特征向量.
(本小题为选做题,满分10分)
如图,AB是半圆的直径,C是AB延长线上一点,CD
切半圆于点D,CD=2,DE⊥AB,垂足为E,且E是
OB的中点,求BC的长.
(本小题满分16分)定义在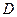 上的函数
上的函数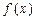 ,如果满足:对任意
,如果满足:对任意 ,存在常数
,存在常数 ,都有
,都有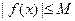 成立,则称
成立,则称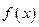 是
是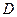 上的有界函数,其中
上的有界函数,其中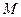 称为函数
称为函数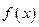 的上界.
的上界.
已知函数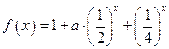 ;
;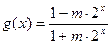 .
.
(1)当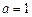 时,求函数
时,求函数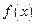 在
在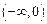 上的值域,并判断函数
上的值域,并判断函数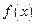 在
在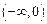 上是否为有界函数,请说明理由;
上是否为有界函数,请说明理由;
(2)若函数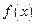 在
在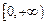 上是以3为上界的有界函数,求实数
上是以3为上界的有界函数,求实数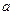 的取值范围;
的取值范围;
(3)若 ,函数
,函数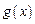 在
在 上的上界是
上的上界是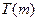 ,求
,求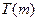 的取值范围.
的取值范围.
(本小题满分16分)设数列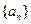 的前n项和为
的前n项和为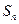 ,数列
,数列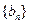 满足:
满足: 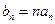 ,且数列
,且数列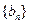 的前
的前
n项和为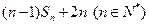 .
.
(1) 求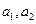 的值;
的值;
(2) 求证:数列 是等比数列;
是等比数列;
(3) 抽去数列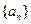 中的第1项,第4项,第7项,……,第3n-2项,……余下的项顺序不变,组成一个新数列
中的第1项,第4项,第7项,……,第3n-2项,……余下的项顺序不变,组成一个新数列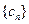 ,若
,若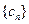 的前n项和为
的前n项和为 ,求证:
,求证: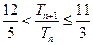 .
.