某研究所计划利用“神七”宇宙飞船进行新产品搭载实验,计划搭载若干件新产品A、B,该所要根据该产品的研制成本、产品重量、搭载实验费用和预计产生的收益来决定具体搭载安排,有关数据如下表:
| |
每件产品A |
每件产品B |
|
| 研制成本、搭载 费用之和(万元) |
20 |
30 |
计划最大资金额 300万元 |
| 产品重量(千克) |
10 |
5 |
最大搭载重量110千克 |
| 预计收益(万元) |
80 |
60 |
|
如何安排这两种产品的搭载件数,才能使总预计收益达到最大,最大收益是多少?
(1)计算: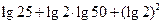
(2)计算 ;
;
(3)设 求
求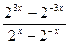 的值
的值
已知:
(1)若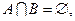 求实数
求实数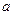 的取值范围。
的取值范围。
(2)若 求实数
求实数 的取值范围。
的取值范围。
(本小题满分12分)
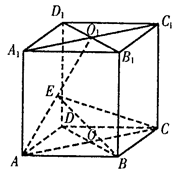
如图,直平行六面体ABCD-A1B1C1D1的高为3,
底面是边长为4, 且∠BAD=60°的菱形,AC∩
BD=O,A1C1∩B1D1=O1,E是线段AO1上一点.
(Ⅰ)求点A到平面O1BC的距离;
(Ⅱ)当AE为何值时,二面角E-BC-D的大小为 .
.
(本小题满分10分)
如图,设A是单位圆和x轴正半轴的交点,P,Q是单
位圆上的两点,D是坐标原点,∠AOP=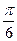 .∠AOQ=α,α∈[0,π).(Ⅰ)若Q(
.∠AOQ=α,α∈[0,π).(Ⅰ)若Q(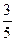 ,
,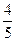 ),求cos(α-
),求cos(α-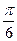 )的值; (Ⅱ)设函数f(α)=
)的值; (Ⅱ)设函数f(α)=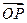 ·
·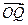 ,求f(α)的值域.
,求f(α)的值域.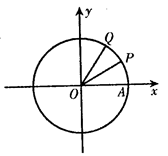
(本小题满分12分)
对于函数f(x),若存在x0∈R,使f(x0)=x0成立,则称x0为f(x)的不动点。如果函数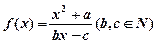 有且只有两个不动点0,2,且
有且只有两个不动点0,2,且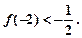
(1)求函数f(x)的解析式;
(2)已知各项不为零的数列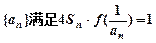 (
(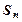 为
为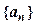 数列前n项和),求数列通项
数列前n项和),求数列通项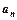 ;
;
(3)如果数列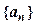 满足
满足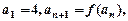 ,求证:当
,求证:当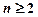 时,恒有
时,恒有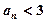 成立.
成立.