已知F1、F2分别是椭圆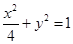 的左、右焦点.
的左、右焦点.
(Ⅰ)若P是第一象限内该图形上的一点,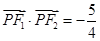 ,求点P的坐标;
,求点P的坐标;
(Ⅱ)设过定点M(0,2)的直线l与椭圆交于同的两点A、B,且∠AOB为锐角(其中O为作标原点),求直线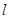 的斜率
的斜率 的取值范围.
的取值范围.
如图所示,直三棱柱ABC—A1B1C1中,CA=CB=1,∠BCA=90°,棱AA1=2,M、N分别是A1B1、A1A的中点.
(1)求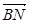 的长;
的长;
(2)求cos< >的值;
>的值;
(3)求证:A1B⊥C1M.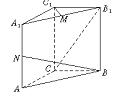
四棱锥P—ABCD中,底面ABCD是一个平行四边形,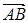 ={2,-1,-4},
={2,-1,-4},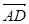 ={4,2,0},
={4,2,0},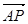 ={-1,2,-1}.
={-1,2,-1}.
(1)求证:PA⊥底面ABCD;
(2)求四棱锥P—ABCD的体积;
(3)对于向量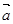 ={x1,y1,z1},
={x1,y1,z1}, ={x2,y2,z2},
={x2,y2,z2},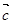 ={x3,y3,z3},定义一种运算:
={x3,y3,z3},定义一种运算:
(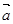 ×
× )·
)·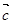 =x1y2z3+x2y3z1+x3y1z2-x1y3z2-x2y1z3-x3y2z1,试计算(
=x1y2z3+x2y3z1+x3y1z2-x1y3z2-x2y1z3-x3y2z1,试计算(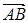 ×
×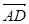 )·
)·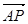 的绝对值的值;说明其与四棱锥P—ABCD体积的关系,并由此猜想向量这一运算(
的绝对值的值;说明其与四棱锥P—ABCD体积的关系,并由此猜想向量这一运算(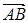 ×
×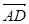 )·
)·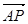 的绝对值的几何意义..
的绝对值的几何意义..
若四面体对应棱的中点间的距离都相等,证明这个四面体的对棱两两垂直.
如图在空间直角坐标系中BC=2,原点O是BC的中点,点A的坐标是( ,0),点D在平面yOz上,且∠BDC=90°,∠DCB=30°.
,0),点D在平面yOz上,且∠BDC=90°,∠DCB=30°.
(1)求向量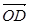 的坐标;
的坐标;
(2)设向量 和
和 的夹角为θ,求cosθ的值
的夹角为θ,求cosθ的值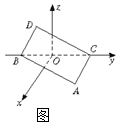
如图,已知正方体 的棱长为a,M为
的棱长为a,M为 的中点,点N在
的中点,点N在 '上,且
'上,且 ,试求MN的长.
,试求MN的长.