选修4-4;坐标系与参数方程
在直角坐标系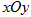 中,以O为极点,x轴正半轴为极轴建立极坐标系.曲线C的极坐标方程为
中,以O为极点,x轴正半轴为极轴建立极坐标系.曲线C的极坐标方程为 ,M,N分别为C与x轴,y轴的交点.
,M,N分别为C与x轴,y轴的交点.
(1)写出C的直角坐标方程,并求M、N的极坐标;
(2)设MN的中点为P,求直线OP的极坐标方程.
先在甲、乙两个靶.某射手向甲靶射击一次,命中的概率为
,命中得1分,没有命中得0分;向乙靶射击两次,每次命中的概率为
,每命中一次得2分,没有命中得0分.该射手每次射击的结果相互独立.假设该射手完成以上三次射击.
(Ⅰ)求该射手恰好命中一次的概率;
(Ⅱ)求该射手的总得分
的分布列及数学期望
.
在如图所示的几何体中,四边形 是等腰梯形, , 平面 .
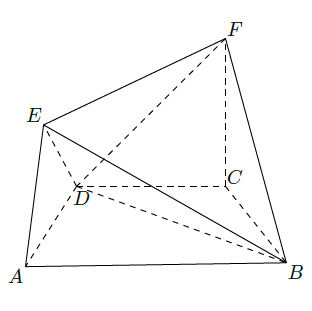
(Ⅰ)求证:
平面
;
(Ⅱ)求二面角
的余弦值.
已知向量
,函数
的最大值为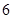 .
.
(Ⅰ)求
;
(Ⅱ)将函数
的图象向左平移
个单位,再将所得图象上各点的横坐标缩短为原来的
倍,纵坐标不变,得到函数
的图象.求
在
上的值域.
在平面直角坐标系中,以坐标原点 为极点, 轴的正半轴为极轴建立极坐标系。已知直线 上两点 的极坐标分别为(2,0)( ),圆 的参数方程
(1)设 为线段 的中点,求直线 的平面直角坐标方程
(2)判断直线 与圆 的位置关系
已知函数
,
,且
的解集为
.
(Ⅰ)求
的值;
(Ⅱ)若
,且
,求证:
.