某日用品按行业质量标准分成五个等级,等级系数X依次为1,2,3,4,5.现从一批该日用品中随机抽取20件,对其等级系数进行统计分析,得到频率分布表如下:
| X |
1 |
2 |
3 |
4 |
5 |
| 频率 |
a |
0.2 |
0.45 |
b |
c |
(1)若所抽取的20件日用品中,等级系数为4的恰有3件,等级系数为5的恰有2件,求a,b,c的值;
(2)在(1)的条件下,将等级系数为4的3件日用品记为 ,等级系数为5的2件日用品记为
,等级系数为5的2件日用品记为 ,现从
,现从 ,
, 这5件日用品中任取两件(假定每件日用品被取出的可能性相同),求这两件日用品的等级系数恰好相等的概率.
这5件日用品中任取两件(假定每件日用品被取出的可能性相同),求这两件日用品的等级系数恰好相等的概率.
已知函数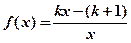
(1)若函数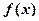 是
是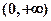 上的增函数,求
上的增函数,求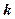 的取值范围;
的取值范围;
(2)证明:当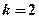 时,不等式
时,不等式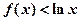 对任意
对任意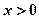 恒成立;
恒成立;
(3)证明: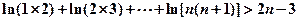
如图,已知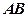
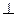 平面
平面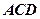 ,
,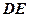 ∥
∥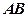 ,
,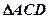 是正三角形,
是正三角形,
且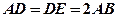 .
.
(1)设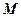 是线段
是线段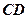 的中点,求证:
的中点,求证: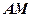 ∥平面
∥平面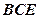 ;
;
(2)求直线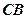 与平面
与平面 所成角的余弦值.
所成角的余弦值.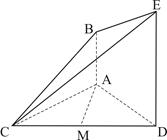
已知数列 满足
满足 ,数列
,数列 满足
满足 .
.
(1)求证:数列 是等差数列;
是等差数列;
(2)设 ,求满足不等式
,求满足不等式 的所有正整数
的所有正整数 的值.
的值.
已知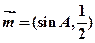 与
与 共线,其中A是△ABC的内角.
共线,其中A是△ABC的内角.
(1)求角A的大小;
(2)若BC=2,求△ABC面积S的最大值,并判断S取得最大值时△ABC的形状.
(本小题满分14分)
已知函数 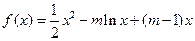 ,
,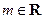 .
.
(Ⅰ)当 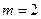 时,求函数
时,求函数 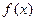 的最小值;
的最小值;
(Ⅱ)当 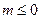 时,讨论函数
时,讨论函数 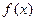 的单调性;
的单调性;
(Ⅲ)求证:当 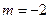 时,对任意的
时,对任意的  ,且
,且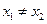 ,有
,有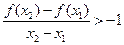 .
.