设数列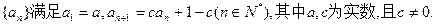
(1)求数列 的通项公式;
的通项公式;
(2)设 ,求数列
,求数列
(3)设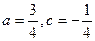 ,
,
 ,记
,记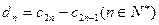 ,设数列
,设数列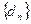 的前
的前 项和为
项和为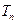 ,求证:对任意正整数
,求证:对任意正整数 都有
都有 ;
;
如图,在三棱锥 中,
中, 底面
底面 ,点
,点 ,
,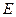 分别在棱
分别在棱 上,且
上,且 (Ⅰ)求证:
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)当 为
为 的中点时,求
的中点时,求 与平面
与平面 所成角的正弦值;
所成角的正弦值;
(Ⅲ)是否存在点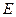 使得二面角
使得二面角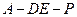 为直二面角?并说明理由.
为直二面角?并说明理由.
有两枚大小相同、质地均匀的正四面体玩具,每个玩具的各个面上分 别写着数字1,2,3,5。同时投掷这两枚玩具一次,记
别写着数字1,2,3,5。同时投掷这两枚玩具一次,记 为两个朝下的面上的数字之和。
为两个朝下的面上的数字之和。
(1)求事件“m不小于6”的概率;
(2)“m为奇数”的概率和“m为偶数”的概率是不是相等?证明你作出的结论。
设 的内角
的内角 所对的边分别为
所对的边分别为 且
且 .(1)求角
.(1)求角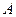 的大小;(2)若
的大小;(2)若 ,求
,求 的周长
的周长 的取值范围.
的取值范围.
各项均为正数的数列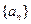 ,
,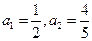 ,且对满足
,且对满足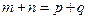 的任意正整
的任意正整
数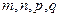 都有
都有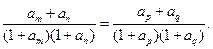
(I)求通项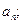
(II)记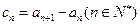 ,设数列
,设数列 的前
的前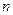 项和为
项和为 ,求证:对任意正整数
,求证:对任意正整数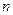 都有
都有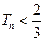 。
。