如图,已知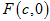 是椭圆
是椭圆 的右焦点,圆
的右焦点,圆 与
与 轴交于
轴交于 两点,其中
两点,其中 是椭圆
是椭圆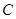 的左焦点.
的左焦点.
(1)求椭圆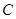 的离心率;
的离心率;
(2)设圆 与
与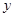 轴的正半轴的交点为
轴的正半轴的交点为 ,点
,点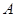 是点
是点 关于
关于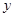 轴的对称点,试判断直线
轴的对称点,试判断直线 与圆
与圆 的位置关系;
的位置关系;
(3)设直线 与圆
与圆 交于另一点
交于另一点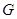 ,若
,若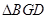 的面积为
的面积为 ,求椭圆
,求椭圆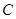 的标准方程.
的标准方程.
已知点P(-3,0),点A在y轴上,点Q在x轴非负半轴上,点M在直线AQ上,满足 ·
· =0,
=0, =-
=-
 .
.
(1)当点A在y轴上移动时,求动点M的轨迹C的方程;
(2)设轨迹C的准线为l,焦点为F,过F作直线m交轨迹C于G,H两点,过点G作平行于轨迹C的对称轴的直线n,且n∩l=E,试问点E,O,H(O为坐标原点)是否在同一条直线上?并说明理由.
如图所示,倾斜角为 的直线经过抛物线y2=8x的焦点F,且与抛物线交于A、B两点.
的直线经过抛物线y2=8x的焦点F,且与抛物线交于A、B两点.
(1)求抛物线焦点F的坐标及准线l的方程;
(2)若 为锐角,作线段AB的垂直平分线m交x轴于点P,证明|FP|-|FP|cos2
为锐角,作线段AB的垂直平分线m交x轴于点P,证明|FP|-|FP|cos2 为定值,
为定值,
并求此定值.
已知抛物线y2=2px(p>0)有一个内接直角三角形,直角顶点在原点,斜边长为2 ,一直角边的方程是y=2x,求抛物线的方程.
,一直角边的方程是y=2x,求抛物线的方程.
已知以向量v= 为方向向量的直线l过点
为方向向量的直线l过点 ,抛物线C:y2=2px(p>0)的顶点关于直线l的对称点在该抛物线的准线上.
,抛物线C:y2=2px(p>0)的顶点关于直线l的对称点在该抛物线的准线上.
(1)求抛物线C的方程;
(2)设A、B是抛物线C上两个动点,过A作平行于x轴的直线m,直线OB与直线m交于点N,若 ·
· +p2="0" (O为原点,A、B异于原点),试求点N的轨迹方程.
+p2="0" (O为原点,A、B异于原点),试求点N的轨迹方程.
已知抛物线顶点在原点,焦点在坐标轴上,又知此抛物线上的一点A(m,-3)到焦点F的距离为5,求m的值,并写出此抛物线的方程.