设数列{an}的前n项和为Sn.已知a1=1,Sn+1=4an+2.
(1)设bn=an+1-2an,证明数列{bn}是等比数列;
(2)求数列{an}的通项公式.
如图,港口A北偏东30°方向的C处有一检查站,港口正东方向的B处有一轮船,距离检查站31海里,该轮船从B处沿正西方向航行20海里后到达D处观测站,已知观测站与检查站距离21海里,问此时轮船离港口A还有多远?
甲、乙两名考生在填报志愿时都选中了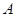 、
、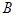 、
、 、
、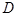 四所需要面试的院校,这四所院校的面试安排在同一时间.因此甲、乙都只能在这四所院校中选择一所做志愿,假设每位同学选择各个院校是等可能的,试求:
四所需要面试的院校,这四所院校的面试安排在同一时间.因此甲、乙都只能在这四所院校中选择一所做志愿,假设每位同学选择各个院校是等可能的,试求:
(Ⅰ)甲、乙选择同一所院校的概率;
(Ⅱ)院校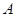 、
、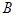 至少有一所被选择的概率.
至少有一所被选择的概率.
已知函数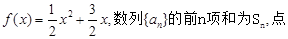
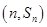 (
(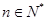 )均在函数
)均在函数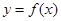 的图象上。
的图象上。
(Ⅰ)求数列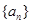 的通项公式
的通项公式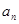 ;
;
(Ⅱ)令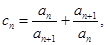 证明:
证明: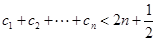
已知函数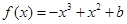 ,
,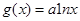
(Ⅰ)若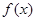 在
在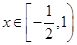 上的最大值为
上的最大值为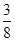 ,求实数b的值;
,求实数b的值;
(Ⅱ)若对任意x∈[1,e],都有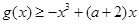 恒成立,求实数a的取值范围;
恒成立,求实数a的取值范围;
(Ⅲ)在(Ⅰ)的条件下,设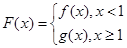 ,对任意给定的正实数a,曲线y=F(x)上是否存在两点P、Q,使得△POQ是以O(O为坐标原点)为直角顶点的直角三角形,且此三角形斜边中点在y轴上?请说明理由.
,对任意给定的正实数a,曲线y=F(x)上是否存在两点P、Q,使得△POQ是以O(O为坐标原点)为直角顶点的直角三角形,且此三角形斜边中点在y轴上?请说明理由.
已知中心在原点,焦点在坐标轴上的椭圆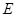 的方程为
的方程为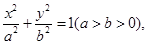 它的离心率为
它的离心率为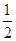 ,一个焦点是
,一个焦点是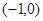 ,过直线
,过直线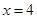 上一点引椭圆
上一点引椭圆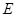 的两条切线,切点分别是A、B.
的两条切线,切点分别是A、B.
(Ⅰ)求椭圆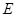 的方程;
的方程;
(Ⅱ)若在椭圆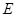
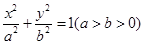 上的点
上的点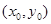 处的切线方程是
处的切线方程是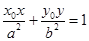 .求证:直线AB恒过定点,并求出定点的坐标;
.求证:直线AB恒过定点,并求出定点的坐标;
(Ⅲ)记点C为(Ⅱ)中直线AB恒过的定点,问否存在实数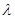 ,使得
,使得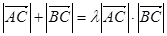 成立,若成立求出
成立,若成立求出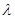 的值,若不存在,请说明理由
的值,若不存在,请说明理由