设函数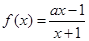 ,其中
,其中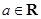 .
.
(1)若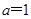 ,
,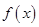 的定义域为区间
的定义域为区间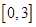 ,求
,求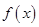 的最大值和最小值;
的最大值和最小值;
(2)若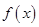 的定义域为区间(0,+∞),求
的定义域为区间(0,+∞),求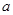 的取值范围,使
的取值范围,使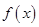 在定义域内是单调减函数.
在定义域内是单调减函数.
如图所示,已知▱ABCD,▱AOBE,▱ACFB,▱ACGD,▱ACDH,点O是▱ABCD的对角线交点,且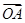 =a,
=a,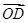 =b,
=b,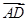 =c.
=c.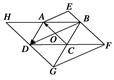
(1)写出图中与a相等的向量;
(2)写出图中与b相等的向量;
(3)写出图中与c相等的向量.
如图所示,4×3的矩形(每个小方格都是单位正方形),在起点和终点都在小方格的顶点处的向量中,试问: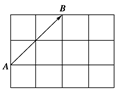
(1)与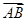 相等的向量共有几个;
相等的向量共有几个;
(2)与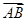 平行且模为
平行且模为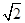 的向量共有几个?
的向量共有几个?
(3)与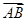 方向相同且模为3
方向相同且模为3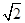 的向量共有几个?
的向量共有几个?
[分析] 非零向量平行(共线)包括两种情况:一种是方向相同,另一种是方向相反.
如图所示,四边形ABCD中,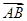 =
=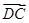 ,N、M是AD、BC上的点,且
,N、M是AD、BC上的点,且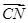 =
= .
.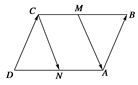
求证: =
=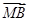 .
.
如图所示,点O为正方形ABCD对角线的交点,四边形OAED,OCFB都是正方形.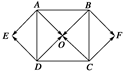
在图中所示的向量中:
(1)分别写出与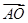 ,
,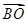 相等的向量;
相等的向量;
(2)写出与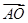 共线的向量;
共线的向量;
(3)写出与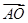 的模相等的向量;
的模相等的向量;
(4)向量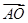 与
与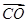 是否相等?
是否相等?
若E,F,M,N分别是四边形ABCD的边AB,BC,CD,DA的中点,求证: =
= .
.