小红将笔记本电脑水平放置在桌子上，显示屏OB与底板OA所在水平线的夹角为120°时，感觉最舒适（如图1），侧面示意图为图2；使用时为了散热，她在底板下面垫入散热架ACO＇后，电脑转到AO＇B＇位置（如图3），侧面示意图为图4．已知OA=OB=24cm，O＇C⊥OA于点C，O＇C=12cm．
（1）求∠CAO＇的度数．
（2）显示屏的顶部B＇比原来升高了多少？
（3）如图4，垫入散热架后，要使显示屏O＇B＇与水平线的夹角仍保持120°，则显示屏O＇B＇应绕点O＇按顺时针方向旋转多少度？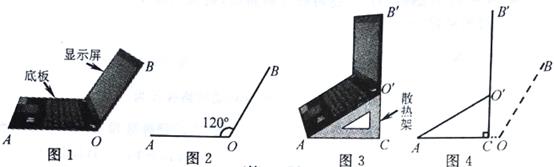
如图，两条公路OA和OB相交于O点，在∠AOB的内部有工厂C和D，现要在∠AOB的内部修建一个货站P，使货站P到两条公路OA、OB的距离相等，且到两工厂C、D的距离相等，用尺规作出货站P的位置．（要求：不写作法，保留作图痕迹，写出结论）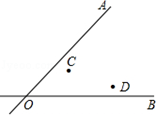
如图，抛物线
与x轴交与A，B两点（点A在点B的左侧），与y轴交于点C．点D和点C关于抛物线的对称轴对称，直线AD与y轴相交于点E．
（1）求直线AD的解析式；
（2）如图1，直线AD上方的抛物线上有一点F，过点F作FG⊥AD于点G，作FH平行于x轴交直线AD于点H，求△FGH的周长的最大值；
（3）点M是抛物线的顶点，点P是y轴上一点，点Q是坐标平面内一点，以A，M，P，Q为顶点的四边形是AM为边的矩形，若点T和点Q关于AM所在直线对称，求点T的坐标．
在△ABC中，AB=AC，∠A=60°，点D是线段BC的中点，∠EDF=120°，DE与线段AB相交于点E，DF与线段AC（或AC的延长线）相交于点F．
（1）如图1，若DF⊥AC，垂足为F，AB=4，求BE的长；
（2）如图2，将（1）中的∠EDF绕点D顺时针旋转一定的角度，DF扔与线段AC相交于点F．求证：
；
（3）如图3，将（2）中的∠EDF继续绕点D顺时针旋转一定的角度，使DF与线段AC的延长线交与点F，作DN⊥AC于点N，若DN=FN，求证：
．
某水库大坝的横截面是如图所示的四边形BACD，期中AB∥CD．瞭望台PC正前方水面上有两艘渔船M、N，观察员在瞭望台顶端P处观测渔船M的俯角
，观测渔船N在俯角
，已知NM所在直线与PC所在直线垂直，垂足为点E，PE长为30米．
（1）求两渔船M，N之间的距离（结果精确到1米）；
（2）已知坝高24米，坝长100米，背水坡AD的坡度
．为提高大坝防洪能力，某施工队在大坝的背水坡填筑土石方加固，加固后坝定加宽3米，背水坡FH的坡度为
，施工12天后，为尽快完成加固任务，施工队增加了机械设备，工作效率提高到原来的1．5倍，结果比原计划提前20天完成加固任务，施工队原计划平均每天填筑土石方多少立方米？（参考数据：
）
如果把一个自然数各数位上数字从最高位到个位依次排出一串数字，与从个位到最高位依次排出的一串数字完全相同，那么我们把这样的自然数叫做 “和谐数”．例如：自然数64746从最高位到个位排出的一串数字是：6、4、7、4、6，从个位到最高排出的一串数字也是：6、4、7、4、6，所64746是“和谐数”．再如：33，181，212，4664，…，都是“和谐数”．
（1）请你直接写出3个四位“和谐数”，猜想任意一个四位“和谐数”能否被11整除，并说明理由；[来。
（2） 已知一个能被11整除的三位“和谐数”，设个位上的数字为x（
，x为自然数），十位上的数字为y，求y与x的函数关系式．