(本小题满分10分)选修4-4:坐标系与参数方程
已知极坐标系的极点与直角坐标系的原点重合,极轴与直角坐标系 轴的正半轴重合.直线的参数方程是
轴的正半轴重合.直线的参数方程是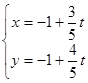 (
( 为参数),曲线
为参数),曲线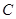 的极坐标方程为
的极坐标方程为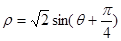 .
.
(Ⅰ)求曲线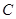 的直角坐标方程;(Ⅱ)设直线与曲线
的直角坐标方程;(Ⅱ)设直线与曲线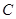 相交于
相交于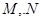 两点,求
两点,求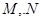 两点间的距离.
两点间的距离.
设函数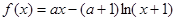 ..
..
(Ⅰ)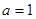 时,求
时,求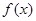 的单调区间;
的单调区间;
(Ⅱ)当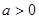 时,设
时,设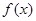 的最小值为
的最小值为 ,若
,若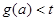 恒成立,求实数t的取值范围.
恒成立,求实数t的取值范围.
如图,在长方体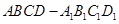 中,
中, ,且
,且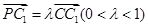 .
.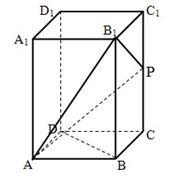
(I)求证:对任意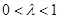 ,总有
,总有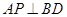 ;
;
(II)若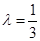 ,求二面角
,求二面角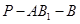 的余弦值;
的余弦值;
(III)是否存在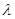 ,使得
,使得 在平面
在平面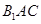 上的射影平分
上的射影平分 ?若存在, 求出
?若存在, 求出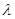 的值, 若不存在,说明理由.
的值, 若不存在,说明理由.
(本小题满分10分)已知中心在原点O,焦点在 轴上的椭圆C的离心率为
轴上的椭圆C的离心率为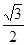 ,点A,B分别是椭圆C的长轴、短轴的端点,点O到直线AB的距离为
,点A,B分别是椭圆C的长轴、短轴的端点,点O到直线AB的距离为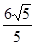 。
。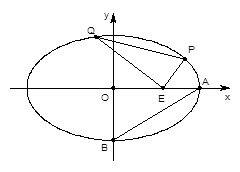
(1)求椭圆C的标准方程;
(2)已知点E(3,0),设点P、Q是椭圆C上的两个动点,满足EP⊥EQ,
求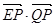 的取值范围.
的取值范围.
(本小题满分10分)河上有一抛物线型拱桥,当水面距拱顶5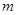 时,水面宽为8
时,水面宽为8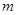 ,一小船宽4
,一小船宽4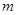 ,高2
,高2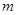 ,载货后船露出水面上的部分高
,载货后船露出水面上的部分高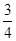
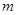 ,问水面上涨到与抛物线拱顶相距多少米时,小船恰好能通行。
,问水面上涨到与抛物线拱顶相距多少米时,小船恰好能通行。