已知f(x)=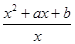 ,
, .
.
(1)若b≥1,求证:函数f(x)在(0,1)上是减函数;
(2)是否存在实数a,b,使f(x)同时满足下列两个条件:
①在(0,1)上是减函数,(1,+∞)上是增函数;
②f(x)的最小值是3.若存在,求出a,b的值;若不存在,请说明理由.
(本小题满分12分)已知△ABC中,角A,B,C的对边分别为a,b,c,且b= c,sinA•cosC=3sinC•cosA.
c,sinA•cosC=3sinC•cosA.
(Ⅰ)若△ABC的面积S= sinA,求c;
sinA,求c;
(Ⅱ)求 的值.
的值.
(本小题满分12分)设向量 =(3,1),
=(3,1), =(-1,2),向量
=(-1,2),向量 垂直于向量
垂直于向量 ,向量
,向量 平行于
平行于 ,试求
,试求 时,
时, 的坐标.
的坐标.
(本小题满分12分)已知函数f(x)=Asin(ωx+φ)(A>0,ω>0, 的部分图像如下图所示:
的部分图像如下图所示:
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)写出函数f(x)的递增区间.
(本小题14分)
已知函数 在
在 处取得极值。
处取得极值。
(Ⅰ)求函数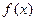 的解析式;
的解析式;
(Ⅱ)求证:对于区间 上任意两个自变量的值
上任意两个自变量的值 ,都有
,都有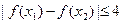 ;
;
(Ⅲ)若过点 可作曲线
可作曲线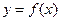 的三条切线,求实数
的三条切线,求实数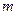 的取值范围。
的取值范围。
(本小题满 分12分)
分12分)
如图所示,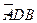 为半圆,AB为半圆直径,O为半圆圆心,且OD⊥AB,Q为线段OD的中点,已知|AB|=4,曲线C过Q点,动点P在曲线C上运动且保持|PA|+|PB|的值不
为半圆,AB为半圆直径,O为半圆圆心,且OD⊥AB,Q为线段OD的中点,已知|AB|=4,曲线C过Q点,动点P在曲线C上运动且保持|PA|+|PB|的值不 变.
变.
(Ⅰ)建立适当的平面直角坐标系,求曲线C的方程;
(Ⅱ)过D点的直线l与曲线C相交于不同的两点M、N,问是否存在这样的直线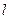 使
使 与
与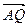 平行,若平行,求出直线
平行,若平行,求出直线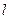 的方程
的方程 , 若不平行,请说明理由.
, 若不平行,请说明理由.