已知函数 为偶函数.
为偶函数.
(1)求 的值;
的值;
(2)若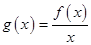 ,当
,当 时,求
时,求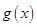 的值域;
的值域;
计算:
某单位为了了解用电量y度与气温x0C之间的关系随机统计了某4天的用电量与当天气温
| 气温(0C) |
14 |
12 |
8 |
6 |
| 用电量 |
22 |
26 |
34 |
38 |
(1)求用电量y与气温x的线性回归方程;
(2)由(1)的方程预测气温为50C时,用电量的度数。
参考公式:
(本小题满分13分)某校学习小组开展“学生语文成绩与外语成绩的关系”的课题研究,对该校高二年级800名学生上学期期末语文和外语成绩,按优秀和不优秀分类得结果:语文和外语都优秀的有60人,语文成绩优秀但外语不优秀的有140人,外语成绩优秀但语文不优秀的有100人.
(Ⅰ)能否在犯错概率不超过0.001的前提下认为该校学生的语文成绩与外语成绩有关系?
(Ⅱ)4名成员随机分成两组,每组2人,一组负责收集成绩,另一组负责数据处理。求学生甲分到负责收集成绩组,学生乙分到负责数据处理组的概率。
 |
0.010 |
0.005 |
0.001 |
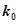 |
6.635 |
7.879 |
10.828 |
附:
(满分10分)已知复数 满足:
满足: 
(1)求 并求其在复平面上对应的点的坐标;
并求其在复平面上对应的点的坐标;
(2)求 的共轭复数E:\WCFUpload\Upload\2015-08\04\04891303-8df8-452b-8372-8b1d9afe39e5\ http:\\
的共轭复数E:\WCFUpload\Upload\2015-08\04\04891303-8df8-452b-8372-8b1d9afe39e5\ http:\\
(满分10分)(1)用分析法证明:当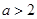 时,
时, ;
;
(2)设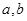 是两个不相等的正数,若
是两个不相等的正数,若 ,用综合法证明:
,用综合法证明: